A Showdown of ChatGPT vs DeepSeek in Solving Programming Tasks

The advancement of large language models (LLMs) has created a competitive landscape for AI-assisted programming tools. This study evaluates two leading models: ChatGPT 03-mini and DeepSeek-R1 on their ability to solve competitive programming tasks from Codeforces. Using 29 programming tasks of three levels of easy, medium, and hard difficulty, we assessed the outcome of both models by their accepted solutions, memory efficiency, and runtime performance. Our results indicate that while both models perform similarly on easy tasks, ChatGPT outperforms DeepSeek-R1 on medium-difficulty tasks, achieving a 54.5% success rate compared to DeepSeek 18.1%. Both models struggled with hard tasks, thus highlighting some ongoing challenges LLMs face in handling highly complex programming problems. These findings highlight key differences in both model capabilities and their computational power, offering valuable insights for developers and researchers working to advance AI-driven programming tools.

Creating Artificial Students that Never Existed: Leveraging Large Language Models and CTGANs for Synthetic Data Generation

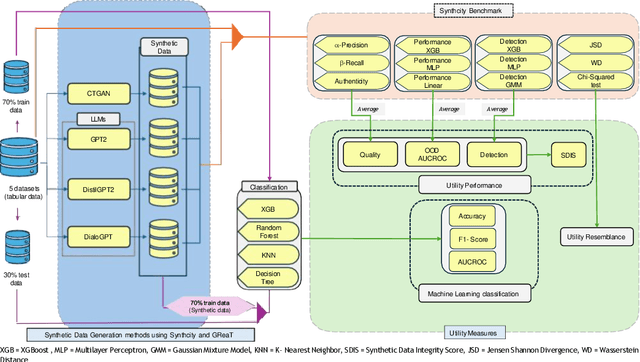
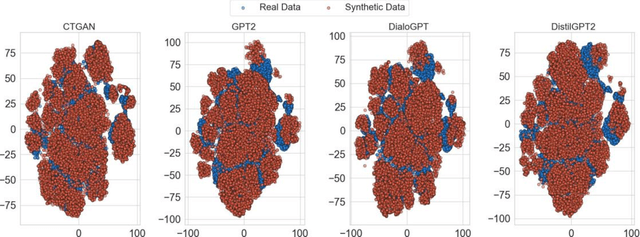
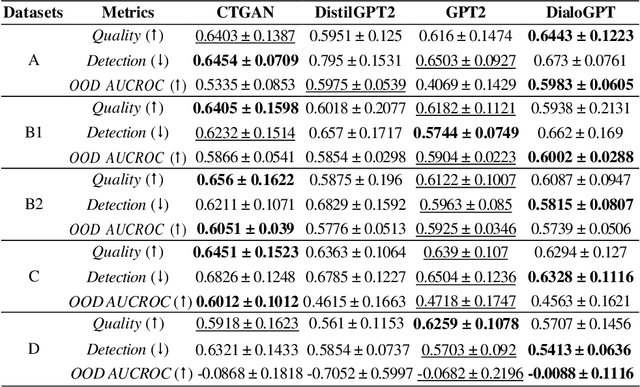
In this study, we explore the growing potential of AI and deep learning technologies, particularly Generative Adversarial Networks (GANs) and Large Language Models (LLMs), for generating synthetic tabular data. Access to quality students data is critical for advancing learning analytics, but privacy concerns and stricter data protection regulations worldwide limit their availability and usage. Synthetic data offers a promising alternative. We investigate whether synthetic data can be leveraged to create artificial students for serving learning analytics models. Using the popular GAN model CTGAN and three LLMs- GPT2, DistilGPT2, and DialoGPT, we generate synthetic tabular student data. Our results demonstrate the strong potential of these methods to produce high-quality synthetic datasets that resemble real students data. To validate our findings, we apply a comprehensive set of utility evaluation metrics to assess the statistical and predictive performance of the synthetic data and compare the different generator models used, specially the performance of LLMs. Our study aims to provide the learning analytics community with valuable insights into the use of synthetic data, laying the groundwork for expanding the field methodological toolbox with new innovative approaches for learning analytics data generation.

Can Synthetic Data be Fair and Private? A Comparative Study of Synthetic Data Generation and Fairness Algorithms

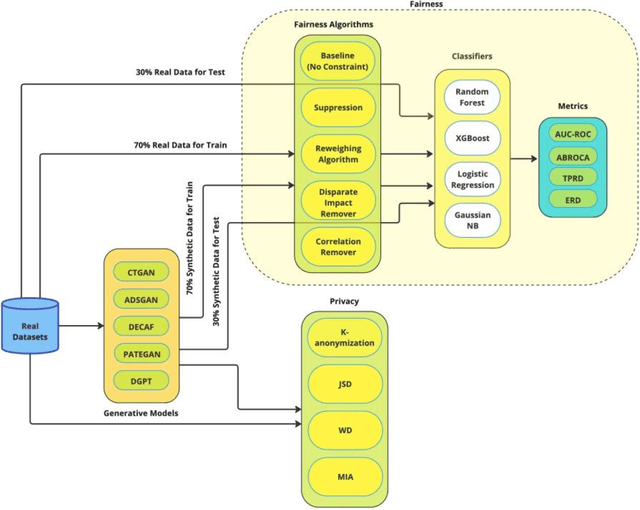
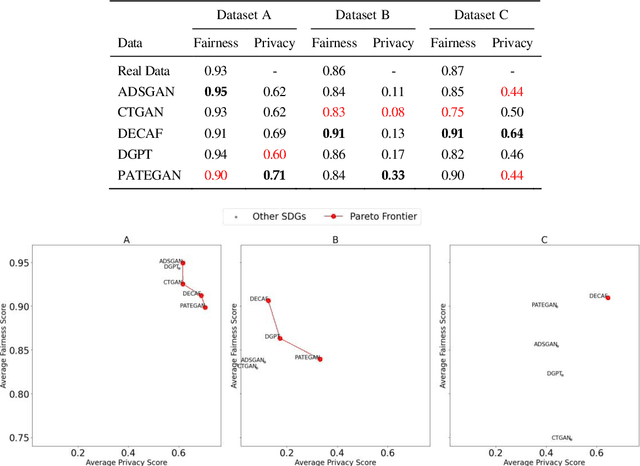
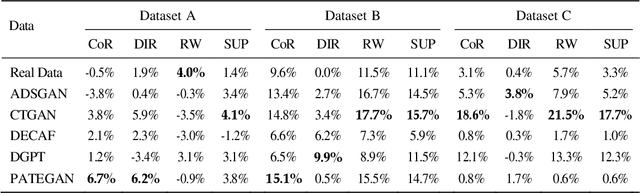
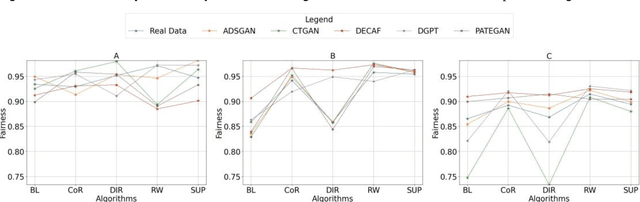
The increasing use of machine learning in learning analytics (LA) has raised significant concerns around algorithmic fairness and privacy. Synthetic data has emerged as a dual-purpose tool, enhancing privacy and improving fairness in LA models. However, prior research suggests an inverse relationship between fairness and privacy, making it challenging to optimize both. This study investigates which synthetic data generators can best balance privacy and fairness, and whether pre-processing fairness algorithms, typically applied to real datasets, are effective on synthetic data. Our results highlight that the DEbiasing CAusal Fairness (DECAF) algorithm achieves the best balance between privacy and fairness. However, DECAF suffers in utility, as reflected in its predictive accuracy. Notably, we found that applying pre-processing fairness algorithms to synthetic data improves fairness even more than when applied to real data. These findings suggest that combining synthetic data generation with fairness pre-processing offers a promising approach to creating fairer LA models.

From Width-Based Model Checking to Width-Based Automated Theorem Proving

In the field of parameterized complexity theory, the study of graph width measures has been intimately connected with the development of width-based model checking algorithms for combinatorial properties on graphs. In this work, we introduce a general framework to convert a large class of width-based model-checking algorithms into algorithms that can be used to test the validity of graph-theoretic conjectures on classes of graphs of bounded width. Our framework is modular and can be applied with respect to several well-studied width measures for graphs, including treewidth and cliquewidth. As a quantitative application of our framework, we show that for several long-standing graph-theoretic conjectures, there exists an algorithm that takes a number $k$ as input and correctly determines in time double-exponential in $k^{O(1)}$ whether the conjecture is valid on all graphs of treewidth at most $k$. This improves significantly on upper bounds obtained using previously available techniques.