Approximate Survey Propagation for Statistical Inference

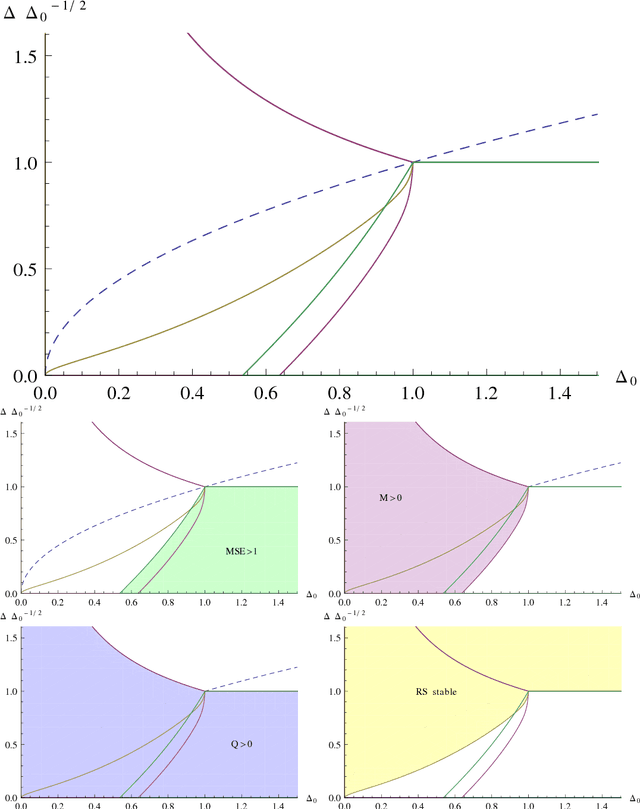
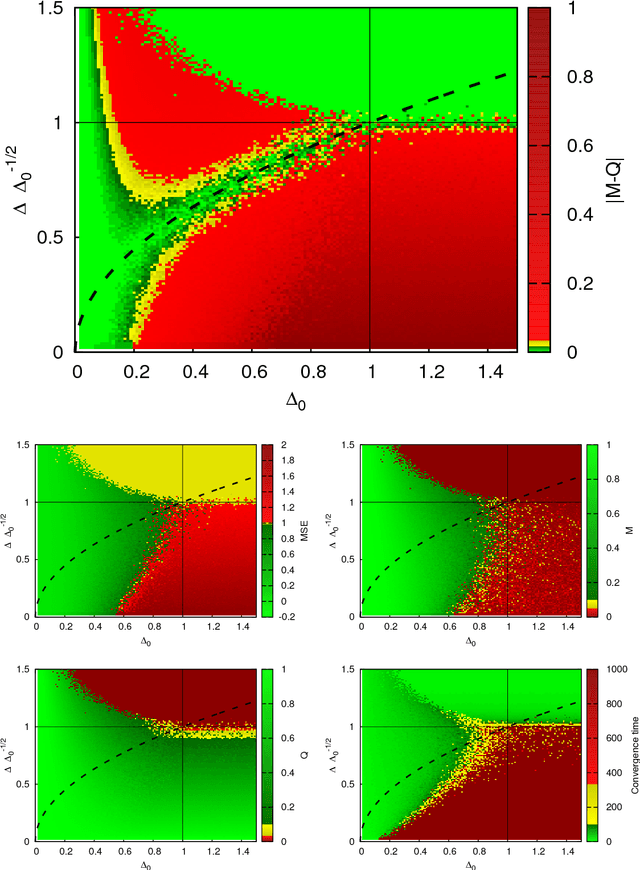
Approximate message passing algorithm enjoyed considerable attention in the last decade. In this paper we introduce a variant of the AMP algorithm that takes into account glassy nature of the system under consideration. We coin this algorithm as the approximate survey propagation (ASP) and derive it for a class of low-rank matrix estimation problems. We derive the state evolution for the ASP algorithm and prove that it reproduces the one-step replica symmetry breaking (1RSB) fixed-point equations, well-known in physics of disordered systems. Our derivation thus gives a concrete algorithmic meaning to the 1RSB equations that is of independent interest. We characterize the performance of ASP in terms of convergence and mean-squared error as a function of the free Parisi parameter s. We conclude that when there is a model mismatch between the true generative model and the inference model, the performance of AMP rapidly degrades both in terms of MSE and of convergence, while ASP converges in a larger regime and can reach lower errors. Among other results, our analysis leads us to a striking hypothesis that whenever s (or other parameters) can be set in such a way that the Nishimori condition $M=Q>0$ is restored, then the corresponding algorithm is able to reach mean-squared error as low as the Bayes-optimal error obtained when the model and its parameters are known and exactly matched in the inference procedure.

On the glassy nature of the hard phase in inference problems

An algorithmically hard phase was described in a range of inference problems: even if the signal can be reconstructed with a small error from an information theoretic point of view, known algorithms fail unless the noise-to-signal ratio is sufficiently small. This hard phase is typically understood as a metastable branch of the dynamical evolution of message passing algorithms. In this work we study the metastable branch for a prototypical inference problem, the low-rank matrix factorization, that presents a hard phase. We show that for noise-to-signal ratios that are below the information theoretic threshold, the posterior measure is composed of an exponential number of metastable glassy states and we compute their entropy, called the complexity. We show that this glassiness extends even slightly below the algorithmic threshold below which the well-known approximate message passing (AMP) algorithm is able to closely reconstruct the signal. Counter-intuitively, we find that the performance of the AMP algorithm is not improved by taking into account the glassy nature of the hard phase.