Approximate Survey Propagation for Statistical Inference
Paper and Code
Jul 03, 2018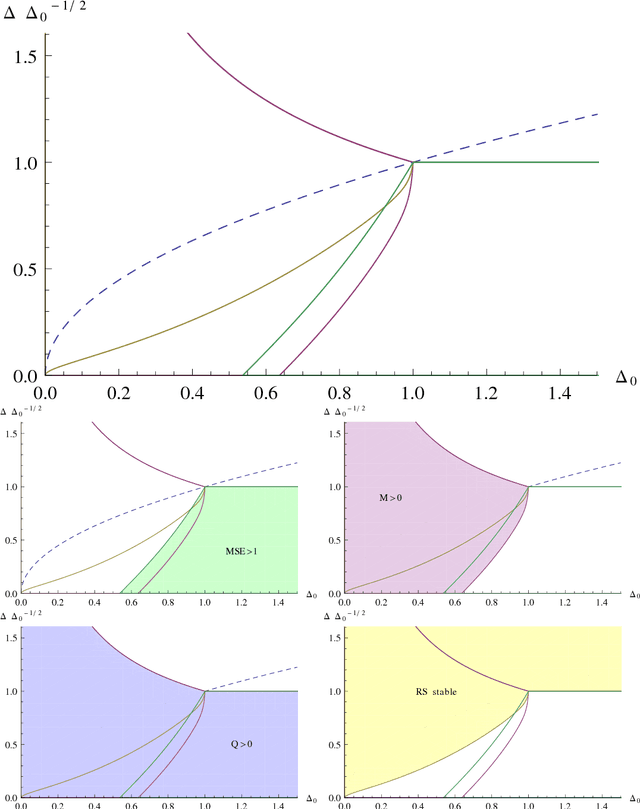
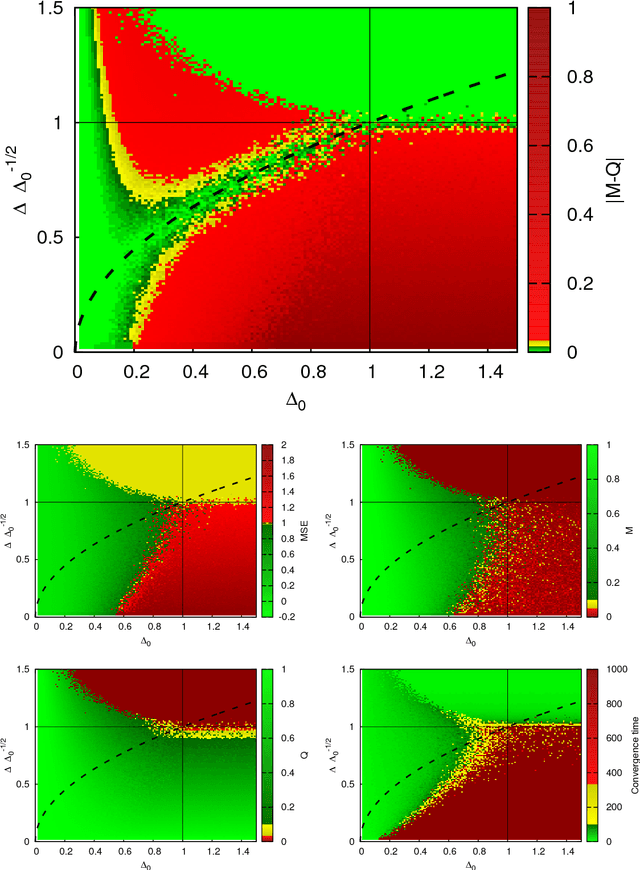


Approximate message passing algorithm enjoyed considerable attention in the last decade. In this paper we introduce a variant of the AMP algorithm that takes into account glassy nature of the system under consideration. We coin this algorithm as the approximate survey propagation (ASP) and derive it for a class of low-rank matrix estimation problems. We derive the state evolution for the ASP algorithm and prove that it reproduces the one-step replica symmetry breaking (1RSB) fixed-point equations, well-known in physics of disordered systems. Our derivation thus gives a concrete algorithmic meaning to the 1RSB equations that is of independent interest. We characterize the performance of ASP in terms of convergence and mean-squared error as a function of the free Parisi parameter s. We conclude that when there is a model mismatch between the true generative model and the inference model, the performance of AMP rapidly degrades both in terms of MSE and of convergence, while ASP converges in a larger regime and can reach lower errors. Among other results, our analysis leads us to a striking hypothesis that whenever s (or other parameters) can be set in such a way that the Nishimori condition $M=Q>0$ is restored, then the corresponding algorithm is able to reach mean-squared error as low as the Bayes-optimal error obtained when the model and its parameters are known and exactly matched in the inference procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge