ViSTa Dataset: Do vision-language models understand sequential tasks?

Using vision-language models (VLMs) as reward models in reinforcement learning holds promise for reducing costs and improving safety. So far, VLM reward models have only been used for goal-oriented tasks, where the agent must reach a particular final outcome. We explore VLMs' potential to supervise tasks that cannot be scored by the final state alone. To this end, we introduce ViSTa, a dataset for evaluating Vision-based understanding of Sequential Tasks. ViSTa comprises over 4,000 videos with step-by-step descriptions in virtual home, Minecraft, and real-world environments. Its novel hierarchical structure -- basic single-step tasks composed into more and more complex sequential tasks -- allows a fine-grained understanding of how well VLMs can judge tasks with varying complexity. To illustrate this, we use ViSTa to evaluate state-of-the-art VLMs, including CLIP, ViCLIP, and GPT-4o. We find that, while they are all good at object recognition, they fail to understand sequential tasks, with only GPT-4o achieving non-trivial performance.

NGD converges to less degenerate solutions than SGD

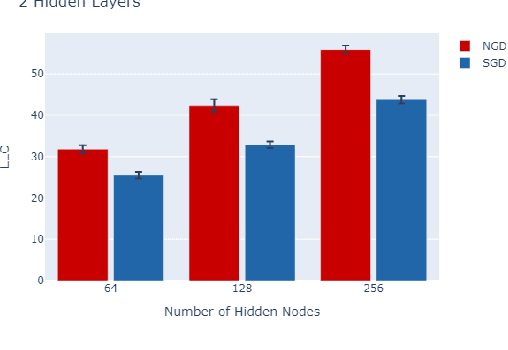
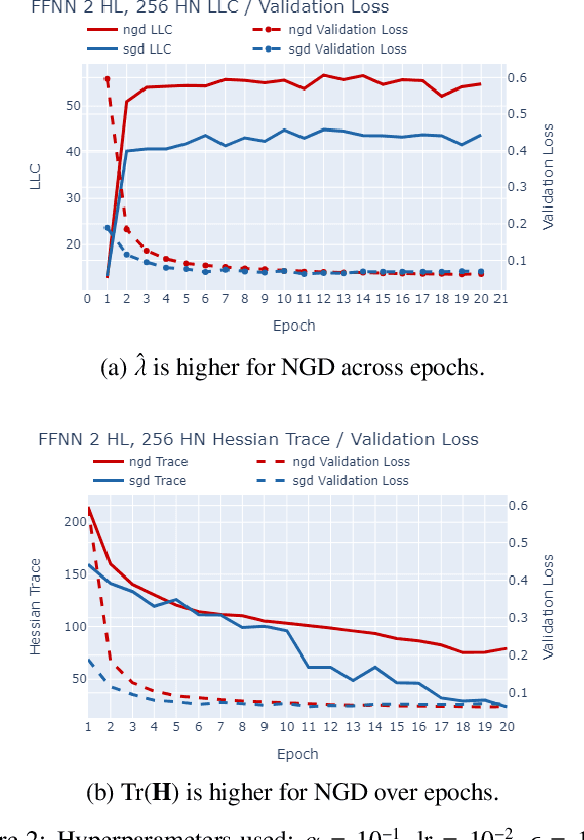
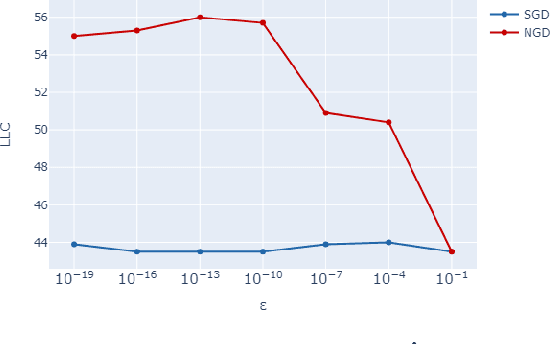
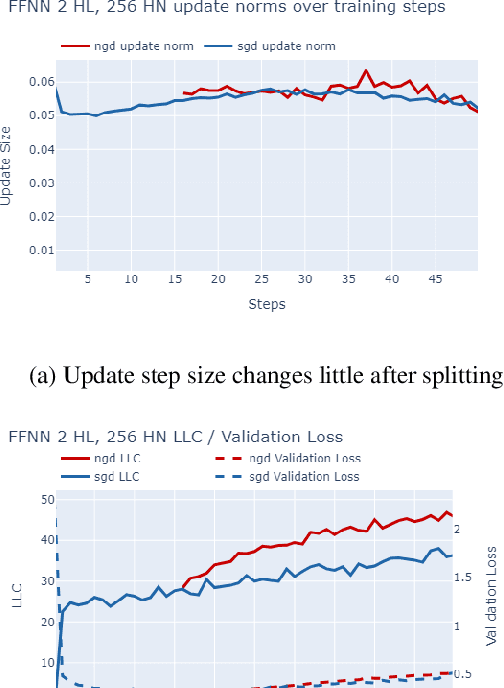
The number of free parameters, or dimension, of a model is a straightforward way to measure its complexity: a model with more parameters can encode more information. However, this is not an accurate measure of complexity: models capable of memorizing their training data often generalize well despite their high dimension. Effective dimension aims to more directly capture the complexity of a model by counting only the number of parameters required to represent the functionality of the model. Singular learning theory (SLT) proposes the learning coefficient $ \lambda $ as a more accurate measure of effective dimension. By describing the rate of increase of the volume of the region of parameter space around a local minimum with respect to loss, $ \lambda $ incorporates information from higher-order terms. We compare $ \lambda $ of models trained using natural gradient descent (NGD) and stochastic gradient descent (SGD), and find that those trained with NGD consistently have a higher effective dimension for both of our methods: the Hessian trace $ \text{Tr}(\mathbf{H}) $, and the estimate of the local learning coefficient (LLC) $ \hat{\lambda}(w^*) $.

Quantifying stability of non-power-seeking in artificial agents

We investigate the question: if an AI agent is known to be safe in one setting, is it also safe in a new setting similar to the first? This is a core question of AI alignment--we train and test models in a certain environment, but deploy them in another, and we need to guarantee that models that seem safe in testing remain so in deployment. Our notion of safety is based on power-seeking--an agent which seeks power is not safe. In particular, we focus on a crucial type of power-seeking: resisting shutdown. We model agents as policies for Markov decision processes, and show (in two cases of interest) that not resisting shutdown is "stable": if an MDP has certain policies which don't avoid shutdown, the corresponding policies for a similar MDP also don't avoid shutdown. We also show that there are natural cases where safety is _not_ stable--arbitrarily small perturbations may result in policies which never shut down. In our first case of interest--near-optimal policies--we use a bisimulation metric on MDPs to prove that small perturbations won't make the agent take longer to shut down. Our second case of interest is policies for MDPs satisfying certain constraints which hold for various models (including language models). Here, we demonstrate a quantitative bound on how fast the probability of not shutting down can increase: by defining a metric on MDPs; proving that the probability of not shutting down, as a function on MDPs, is lower semicontinuous; and bounding how quickly this function decreases.