Moosa Saghir
NGD converges to less degenerate solutions than SGD
Sep 07, 2024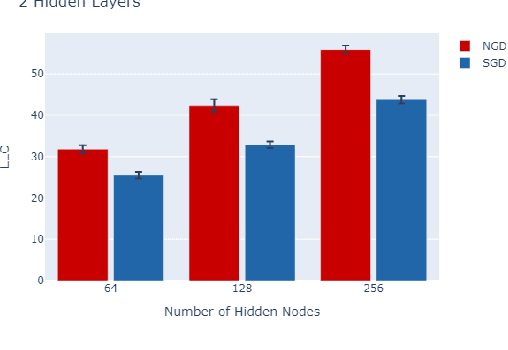
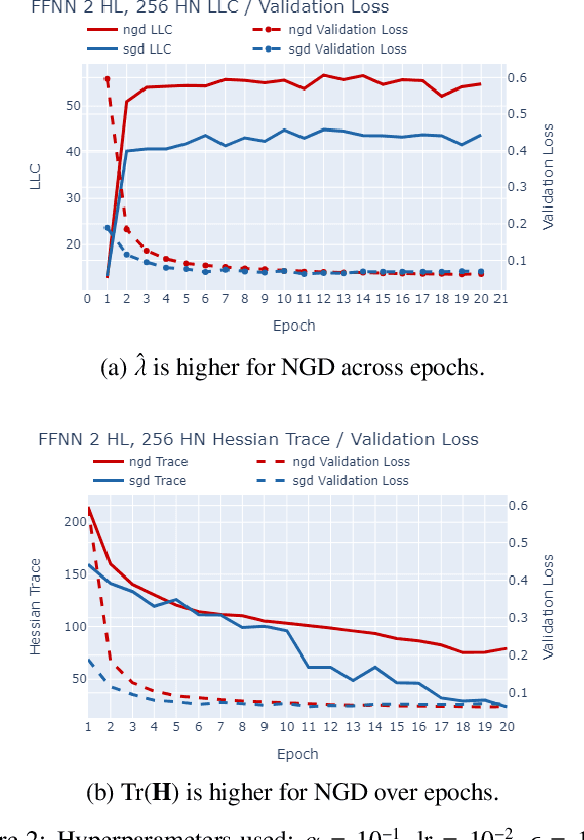
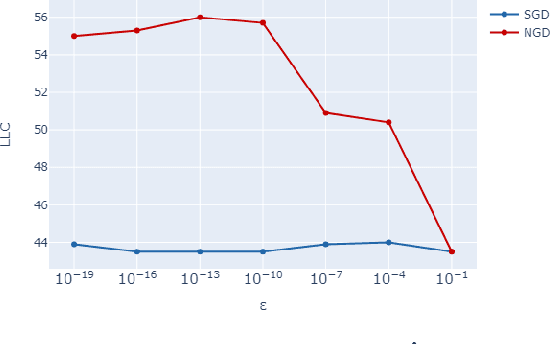
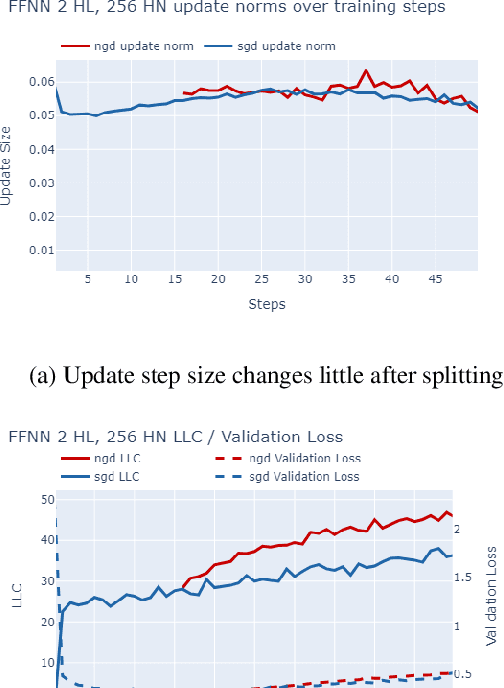
Abstract:The number of free parameters, or dimension, of a model is a straightforward way to measure its complexity: a model with more parameters can encode more information. However, this is not an accurate measure of complexity: models capable of memorizing their training data often generalize well despite their high dimension. Effective dimension aims to more directly capture the complexity of a model by counting only the number of parameters required to represent the functionality of the model. Singular learning theory (SLT) proposes the learning coefficient $ \lambda $ as a more accurate measure of effective dimension. By describing the rate of increase of the volume of the region of parameter space around a local minimum with respect to loss, $ \lambda $ incorporates information from higher-order terms. We compare $ \lambda $ of models trained using natural gradient descent (NGD) and stochastic gradient descent (SGD), and find that those trained with NGD consistently have a higher effective dimension for both of our methods: the Hessian trace $ \text{Tr}(\mathbf{H}) $, and the estimate of the local learning coefficient (LLC) $ \hat{\lambda}(w^*) $.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge