Integral Transforms in a Physics-Informed (Quantum) Neural Network setting: Applications & Use-Cases

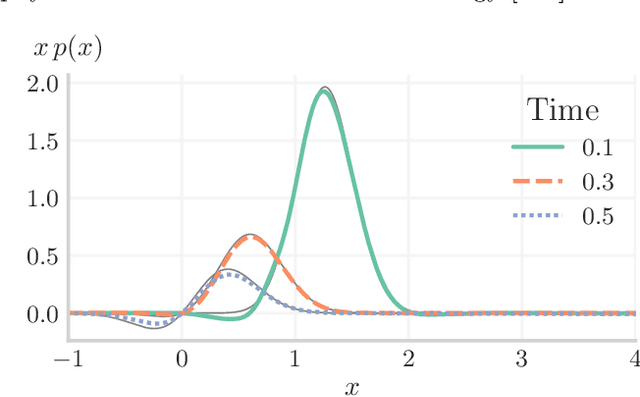
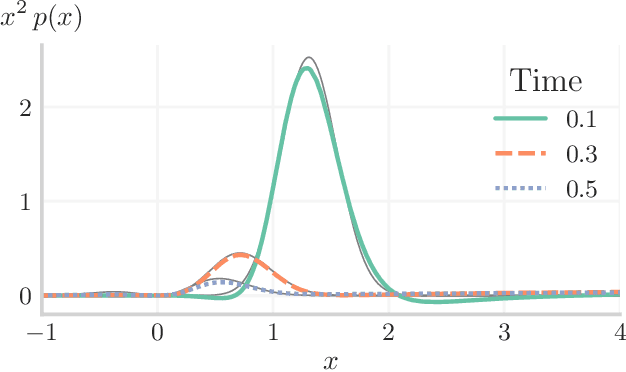
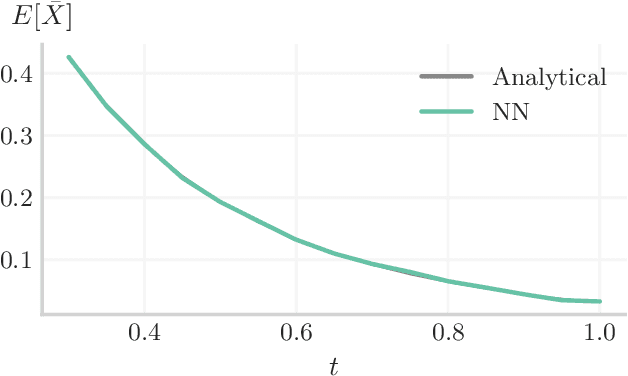
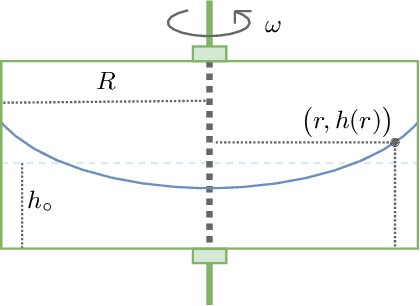
In many computational problems in engineering and science, function or model differentiation is essential, but also integration is needed. An important class of computational problems include so-called integro-differential equations which include both integrals and derivatives of a function. In another example, stochastic differential equations can be written in terms of a partial differential equation of a probability density function of the stochastic variable. To learn characteristics of the stochastic variable based on the density function, specific integral transforms, namely moments, of the density function need to be calculated. Recently, the machine learning paradigm of Physics-Informed Neural Networks emerged with increasing popularity as a method to solve differential equations by leveraging automatic differentiation. In this work, we propose to augment the paradigm of Physics-Informed Neural Networks with automatic integration in order to compute complex integral transforms on trained solutions, and to solve integro-differential equations where integrals are computed on-the-fly during training. Furthermore, we showcase the techniques in various application settings, numerically simulating quantum computer-based neural networks as well as classical neural networks.

Quantum Extremal Learning

We propose a quantum algorithm for `extremal learning', which is the process of finding the input to a hidden function that extremizes the function output, without having direct access to the hidden function, given only partial input-output (training) data. The algorithm, called quantum extremal learning (QEL), consists of a parametric quantum circuit that is variationally trained to model data input-output relationships and where a trainable quantum feature map, that encodes the input data, is analytically differentiated in order to find the coordinate that extremizes the model. This enables the combination of established quantum machine learning modelling with established quantum optimization, on a single circuit/quantum computer. We have tested our algorithm on a range of classical datasets based on either discrete or continuous input variables, both of which are compatible with the algorithm. In case of discrete variables, we test our algorithm on synthetic problems formulated based on Max-Cut problem generators and also considering higher order correlations in the input-output relationships. In case of the continuous variables, we test our algorithm on synthetic datasets in 1D and simple ordinary differential functions. We find that the algorithm is able to successfully find the extremal value of such problems, even when the training dataset is sparse or a small fraction of the input configuration space. We additionally show how the algorithm can be used for much more general cases of higher dimensionality, complex differential equations, and with full flexibility in the choice of both modeling and optimization ansatz. We envision that due to its general framework and simple construction, the QEL algorithm will be able to solve a wide variety of applications in different fields, opening up areas of further research.