Integral Transforms in a Physics-Informed (Quantum) Neural Network setting: Applications & Use-Cases

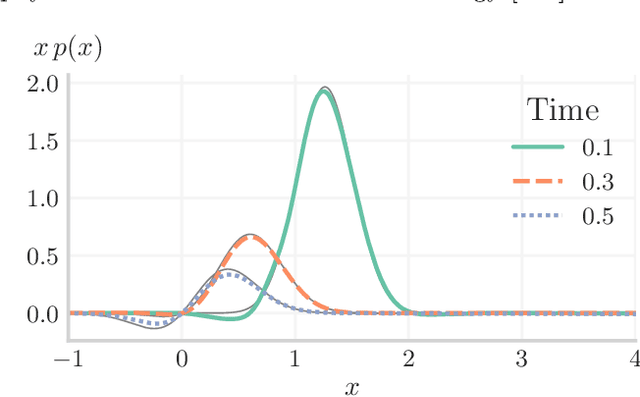
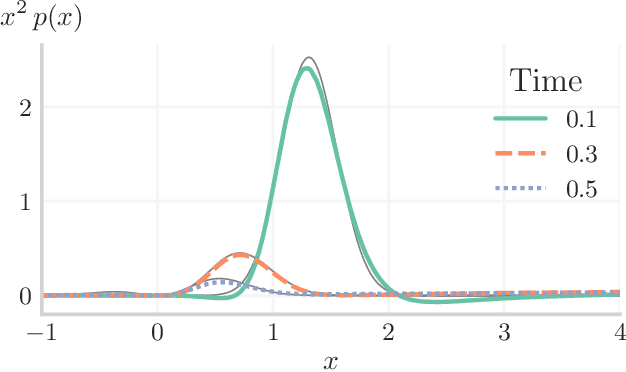
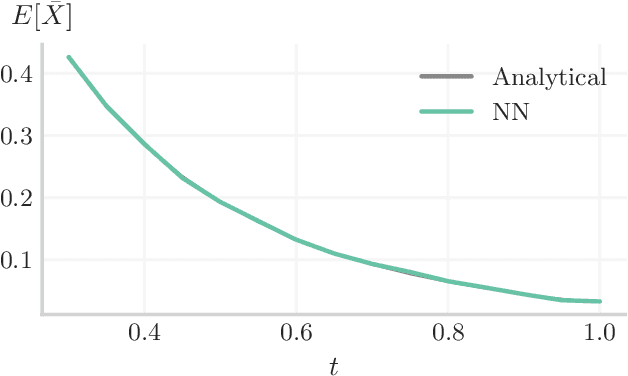
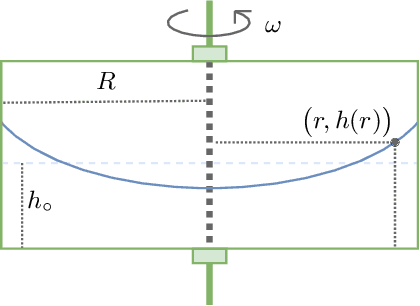
In many computational problems in engineering and science, function or model differentiation is essential, but also integration is needed. An important class of computational problems include so-called integro-differential equations which include both integrals and derivatives of a function. In another example, stochastic differential equations can be written in terms of a partial differential equation of a probability density function of the stochastic variable. To learn characteristics of the stochastic variable based on the density function, specific integral transforms, namely moments, of the density function need to be calculated. Recently, the machine learning paradigm of Physics-Informed Neural Networks emerged with increasing popularity as a method to solve differential equations by leveraging automatic differentiation. In this work, we propose to augment the paradigm of Physics-Informed Neural Networks with automatic integration in order to compute complex integral transforms on trained solutions, and to solve integro-differential equations where integrals are computed on-the-fly during training. Furthermore, we showcase the techniques in various application settings, numerically simulating quantum computer-based neural networks as well as classical neural networks.