Symmetry Breaking in Transformers for Efficient and Interpretable Training

The attention mechanism in its standard implementation contains extraneous rotational degrees of freedom that are carried through computation but do not affect model activations or outputs. We introduce a simple symmetry-breaking protocol that inserts a preferred direction into this rotational space through batchwise-sampled, unlearned query and value biases. This modification has two theoretically motivated and empirically validated consequences. First, it can substantially improve the performance of simple, memory-efficient optimizers, narrowing -- and in some cases closing -- the gap to successful but more complex memory-intensive adaptive methods. We demonstrate this by pretraining 124M parameter transformer models with four optimization algorithms (AdamW, SOAP, SGDM, and Energy Conserving Descent(ECD)) and evaluating both validation loss and downstream logical reasoning. Second, it enables an interpretable use of otherwise redundant rotational degrees of freedom, selectively amplifying semantically meaningful token classes within individual attention heads. Overall, our results show that minimal, principled architectural changes can simultaneously improve performance and interpretability.

Improving Energy Conserving Descent for Machine Learning: Theory and Practice

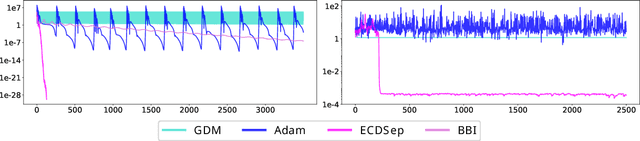
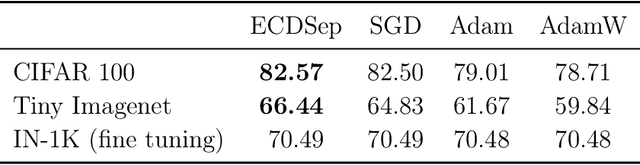
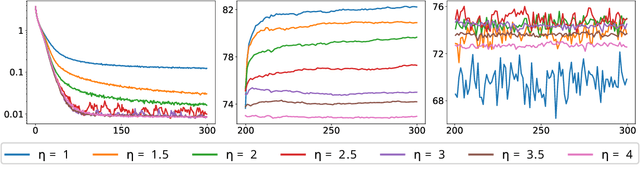
We develop the theory of Energy Conserving Descent (ECD) and introduce ECDSep, a gradient-based optimization algorithm able to tackle convex and non-convex optimization problems. The method is based on the novel ECD framework of optimization as physical evolution of a suitable chaotic energy-conserving dynamical system, enabling analytic control of the distribution of results - dominated at low loss - even for generic high-dimensional problems with no symmetries. Compared to previous realizations of this idea, we exploit the theoretical control to improve both the dynamics and chaos-inducing elements, enhancing performance while simplifying the hyper-parameter tuning of the optimization algorithm targeted to different classes of problems. We empirically compare with popular optimization methods such as SGD, Adam and AdamW on a wide range of machine learning problems, finding competitive or improved performance compared to the best among them on each task. We identify limitations in our analysis pointing to possibilities for additional improvements.

Born-Infeld for AI: Energy-Conserving Descent for Optimization

We introduce a novel framework for optimization based on energy-conserving Hamiltonian dynamics in a strongly mixing (chaotic) regime and establish its key properties analytically and numerically. The prototype is a discretization of Born-Infeld dynamics, with a squared relativistic speed limit depending on the objective function. This class of frictionless, energy-conserving optimizers proceeds unobstructed until slowing naturally near the minimal loss, which dominates the phase space volume of the system. Building from studies of chaotic systems such as dynamical billiards, we formulate a specific algorithm with good performance on machine learning and PDE-solving tasks, including generalization. It cannot stop at a high local minimum and cannot overshoot the global minimum, yielding an advantage in non-convex loss functions, and proceeds faster than GD+momentum in shallow valleys.