Improving Energy Conserving Descent for Machine Learning: Theory and Practice
Paper and Code
Jun 01, 2023
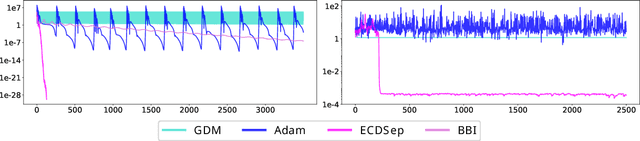
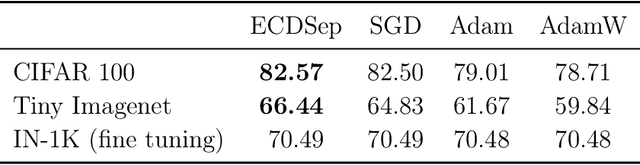
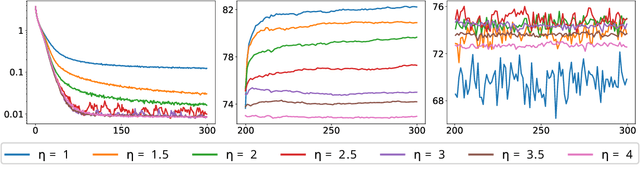
We develop the theory of Energy Conserving Descent (ECD) and introduce ECDSep, a gradient-based optimization algorithm able to tackle convex and non-convex optimization problems. The method is based on the novel ECD framework of optimization as physical evolution of a suitable chaotic energy-conserving dynamical system, enabling analytic control of the distribution of results - dominated at low loss - even for generic high-dimensional problems with no symmetries. Compared to previous realizations of this idea, we exploit the theoretical control to improve both the dynamics and chaos-inducing elements, enhancing performance while simplifying the hyper-parameter tuning of the optimization algorithm targeted to different classes of problems. We empirically compare with popular optimization methods such as SGD, Adam and AdamW on a wide range of machine learning problems, finding competitive or improved performance compared to the best among them on each task. We identify limitations in our analysis pointing to possibilities for additional improvements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge