Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Machine Learning Gravity Compactifications on Negatively Curved Manifolds

Constructing the landscape of vacua of higher-dimensional theories of gravity by directly solving the low-energy (semi-)classical equations of motion is notoriously difficult. In this work, we investigate the feasibility of Machine Learning techniques as tools for solving the equations of motion for general warped gravity compactifications. As a proof-of-concept we use Neural Networks to solve the Einstein PDEs on non-trivial three manifolds obtained by filling one or more cusps of hyperbolic manifolds. While in three dimensions an Einstein metric is also locally hyperbolic, the generality and scalability of Machine Learning methods, the availability of explicit families of hyperbolic manifolds in higher dimensions, and the universality of the filling procedure strongly suggest that the methods and code developed in this work can be of broader applicability. Specifically, they can be used to tackle both the geometric problem of numerically constructing novel higher-dimensional negatively curved Einstein metrics, as well as the physical problem of constructing four-dimensional de Sitter compactifications of M-theory on the same manifolds.

Improving Energy Conserving Descent for Machine Learning: Theory and Practice

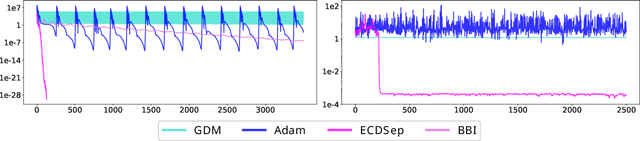
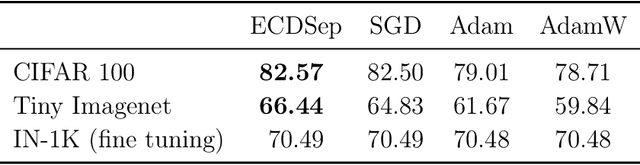
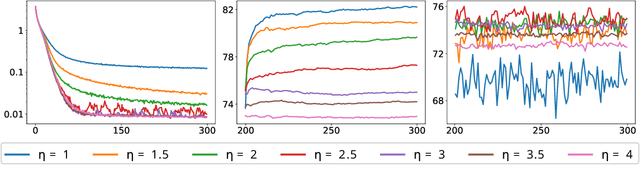
We develop the theory of Energy Conserving Descent (ECD) and introduce ECDSep, a gradient-based optimization algorithm able to tackle convex and non-convex optimization problems. The method is based on the novel ECD framework of optimization as physical evolution of a suitable chaotic energy-conserving dynamical system, enabling analytic control of the distribution of results - dominated at low loss - even for generic high-dimensional problems with no symmetries. Compared to previous realizations of this idea, we exploit the theoretical control to improve both the dynamics and chaos-inducing elements, enhancing performance while simplifying the hyper-parameter tuning of the optimization algorithm targeted to different classes of problems. We empirically compare with popular optimization methods such as SGD, Adam and AdamW on a wide range of machine learning problems, finding competitive or improved performance compared to the best among them on each task. We identify limitations in our analysis pointing to possibilities for additional improvements.

Born-Infeld for AI: Energy-Conserving Descent for Optimization

We introduce a novel framework for optimization based on energy-conserving Hamiltonian dynamics in a strongly mixing (chaotic) regime and establish its key properties analytically and numerically. The prototype is a discretization of Born-Infeld dynamics, with a squared relativistic speed limit depending on the objective function. This class of frictionless, energy-conserving optimizers proceeds unobstructed until slowing naturally near the minimal loss, which dominates the phase space volume of the system. Building from studies of chaotic systems such as dynamical billiards, we formulate a specific algorithm with good performance on machine learning and PDE-solving tasks, including generalization. It cannot stop at a high local minimum and cannot overshoot the global minimum, yielding an advantage in non-convex loss functions, and proceeds faster than GD+momentum in shallow valleys.