Explore to Generalize in Zero-Shot RL

We study zero-shot generalization in reinforcement learning - optimizing a policy on a set of training tasks such that it will perform well on a similar but unseen test task. To mitigate overfitting, previous work explored different notions of invariance to the task. However, on problems such as the ProcGen Maze, an adequate solution that is invariant to the task visualization does not exist, and therefore invariance-based approaches fail. Our insight is that learning a policy that $\textit{explores}$ the domain effectively is harder to memorize than a policy that maximizes reward for a specific task, and therefore we expect such learned behavior to generalize well; we indeed demonstrate this empirically on several domains that are difficult for invariance-based approaches. Our $\textit{Explore to Generalize}$ algorithm (ExpGen) builds on this insight: We train an additional ensemble of agents that optimize reward. At test time, either the ensemble agrees on an action, and we generalize well, or we take exploratory actions, which are guaranteed to generalize and drive us to a novel part of the state space, where the ensemble may potentially agree again. We show that our approach is the state-of-the-art on several tasks in the ProcGen challenge that have so far eluded effective generalization. For example, we demonstrate a success rate of $82\%$ on the Maze task and $74\%$ on Heist with $200$ training levels.

Regularization Guarantees Generalization in Bayesian Reinforcement Learning through Algorithmic Stability

In the Bayesian reinforcement learning (RL) setting, a prior distribution over the unknown problem parameters -- the rewards and transitions -- is assumed, and a policy that optimizes the (posterior) expected return is sought. A common approximation, which has been recently popularized as meta-RL, is to train the agent on a sample of $N$ problem instances from the prior, with the hope that for large enough $N$, good generalization behavior to an unseen test instance will be obtained. In this work, we study generalization in Bayesian RL under the probably approximately correct (PAC) framework, using the method of algorithmic stability. Our main contribution is showing that by adding regularization, the optimal policy becomes stable in an appropriate sense. Most stability results in the literature build on strong convexity of the regularized loss -- an approach that is not suitable for RL as Markov decision processes (MDPs) are not convex. Instead, building on recent results of fast convergence rates for mirror descent in regularized MDPs, we show that regularized MDPs satisfy a certain quadratic growth criterion, which is sufficient to establish stability. This result, which may be of independent interest, allows us to study the effect of regularization on generalization in the Bayesian RL setting.

Deep Residual Flow for Novelty Detection

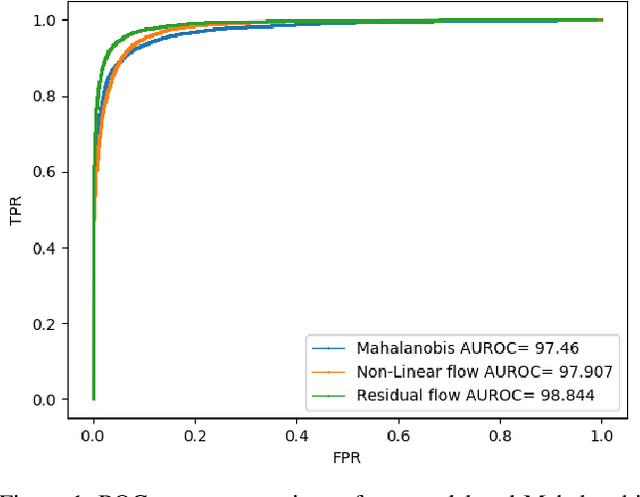
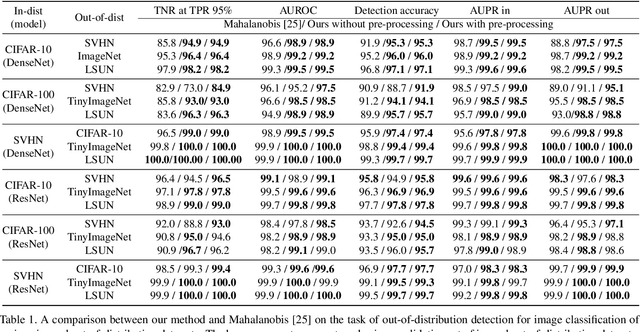
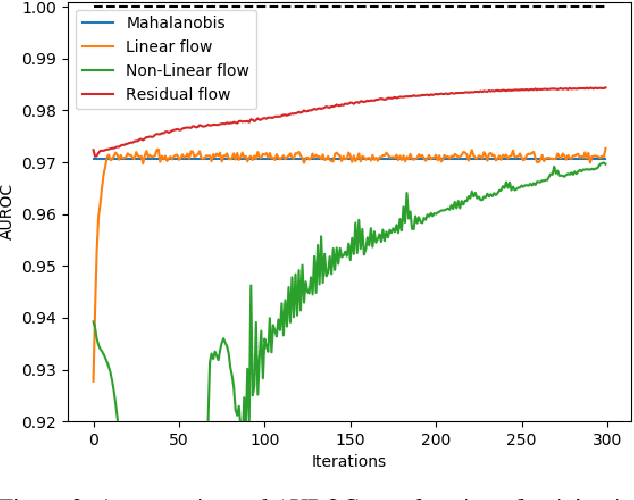
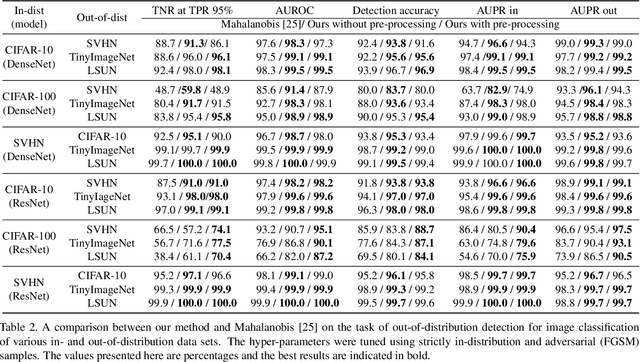
The effective application of neural networks in the real-world relies on proficiently detecting out-of-distribution examples. Contemporary methods seek to model the distribution of feature activations in the training data for adequately distinguishing abnormalities, and the state-of-the-art method uses Gaussian distribution models. In this work, we present a novel approach that improves upon the state-of-the-art by leveraging an expressive density model based on normalizing flows. We introduce the residual flow, a novel flow architecture that learns the residual distribution from a base Gaussian distribution. Our model is general, and can be applied to any data that is approximately Gaussian. For novelty detection in image datasets, our approach provides a principled improvement over the state-of-the-art. Specifically, we demonstrate the effectiveness of our method in ResNet and DenseNet architectures trained on various image datasets. For example, on a ResNet trained on CIFAR-100 and evaluated on detection of out-of-distribution samples from the ImageNet dataset, holding the true positive rate (TPR) at $95\%$, we improve the true negative rate (TNR) from $56.7\%$ (current state-of-the-art) to $77.5\%$ (ours).

A Local Block Coordinate Descent Algorithm for the Convolutional Sparse Coding Model

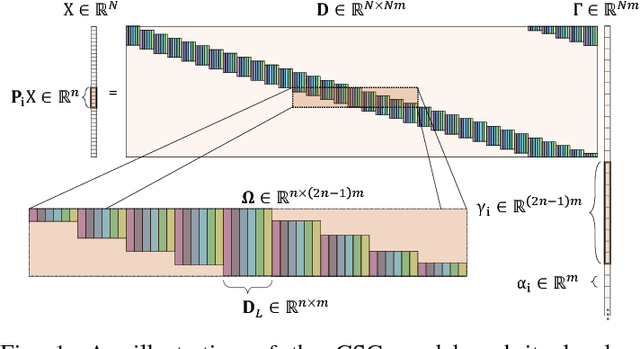
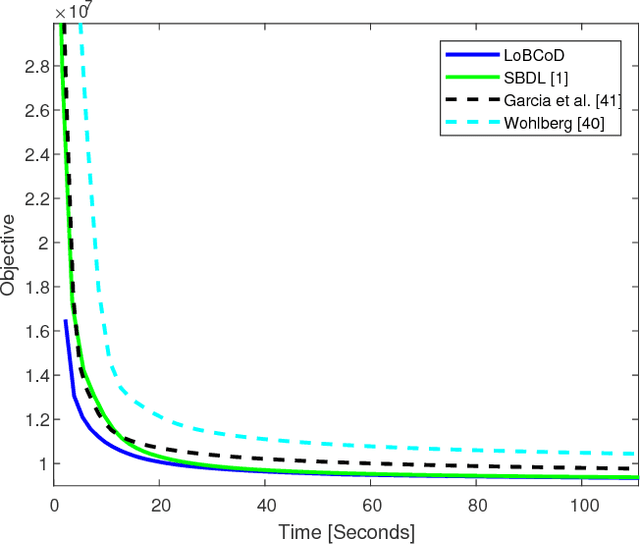
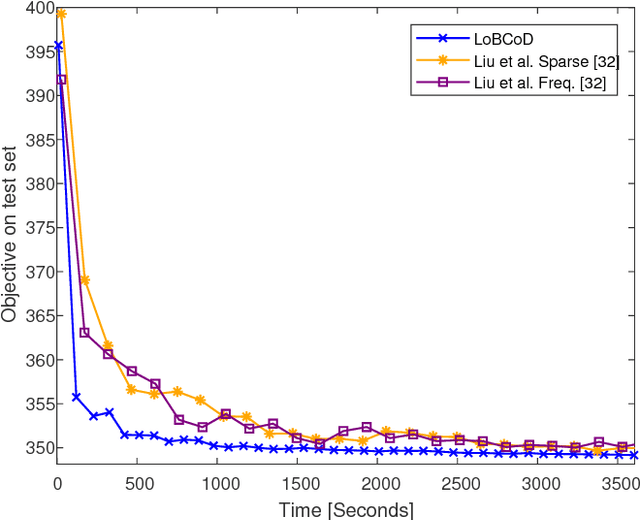
The Convolutional Sparse Coding (CSC) model has recently gained considerable traction in the signal and image processing communities. By providing a global, yet tractable, model that operates on the whole image, the CSC was shown to overcome several limitations of the patch-based sparse model while achieving superior performance in various applications. Contemporary methods for pursuit and learning the CSC dictionary often rely on the Alternating Direction Method of Multipliers (ADMM) in the Fourier domain for the computational convenience of convolutions, while ignoring the local characterizations of the image. A recent work by Papyan et al. suggested the SBDL algorithm for the CSC, while operating locally on image patches. SBDL demonstrates better performance compared to the Fourier-based methods, albeit still relying on the ADMM. In this work we maintain the localized strategy of the SBDL, while proposing a new and much simpler approach based on the Block Coordinate Descent algorithm - this method is termed Local Block Coordinate Descent (LoBCoD). Furthermore, we introduce a novel stochastic gradient descent version of LoBCoD for training the convolutional filters. The Stochastic-LoBCoD leverages the benefits of online learning, while being applicable to a single training image. We demonstrate the advantages of the proposed algorithms for image inpainting and multi-focus image fusion, achieving state-of-the-art results.