TOTOPO: Classifying univariate and multivariate time series with Topological Data Analysis

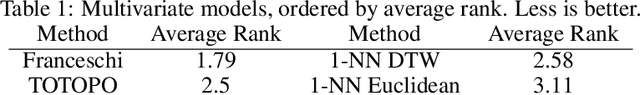
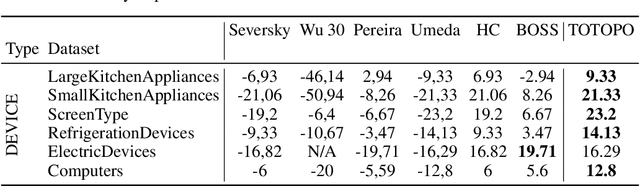
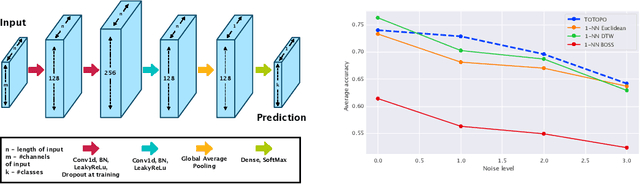
This work is devoted to a comprehensive analysis of topological data analysis fortime series classification. Previous works have significant shortcomings, such aslack of large-scale benchmarking or missing state-of-the-art methods. In this work,we propose TOTOPO for extracting topological descriptors from different types ofpersistence diagrams. The results suggest that TOTOPO significantly outperformsexisting baselines in terms of accuracy. TOTOPO is also competitive with thestate-of-the-art, being the best on 20% of univariate and 40% of multivariate timeseries datasets. This work validates the hypothesis that TDA-based approaches arerobust to small perturbations in data and are useful for cases where periodicity andshape help discriminate between classes.

Are Hyperbolic Representations in Graphs Created Equal?

Recently there was an increasing interest in applications of graph neural networks in non-Euclidean geometry; however, are non-Euclidean representations always useful for graph learning tasks? For different problems such as node classification and link prediction we compute hyperbolic embeddings and conclude that for tasks that require global prediction consistency it might be useful to use non-Euclidean embeddings, while for other tasks Euclidean models are superior. To do so we first fix an issue of the existing models associated with the optimization process at zero curvature. Current hyperbolic models deal with gradients at the origin in ad-hoc manner, which is inefficient and can lead to numerical instabilities. We solve the instabilities of kappa-Stereographic model at zero curvature cases and evaluate the approach of embedding graphs into the manifold in several graph representation learning tasks.