Adversarial Optimal Transport Through The Convolution Of Kernels With Evolving Measures

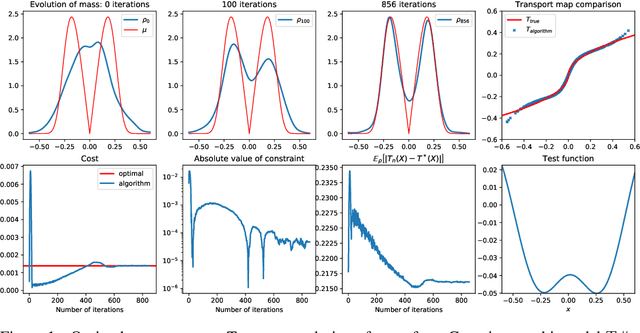
A novel algorithm is proposed to solve the sample-based optimal transport problem. An adversarial formulation of the push-forward condition uses a test function built as a convolution between an adaptive kernel and an evolving probability distribution $\nu$ over a latent variable $b$. Approximating this convolution by its simulation over evolving samples $b^i(t)$ of $\nu$, the parameterization of the test function reduces to determining the flow of these samples. This flow, discretized over discrete time steps $t_n$, is built from the composition of elementary maps. The optimal transport also follows a flow that, by duality, must follow the gradient of the test function. The representation of the test function as the Monte Carlo simulation of a distribution makes the algorithm robust to dimensionality, and its evolution under a memory-less flow produces rich, complex maps from simple parametric transformations. The algorithm is illustrated with numerical examples.

Time-Series Analysis via Low-Rank Matrix Factorization Applied to Infant-Sleep Data

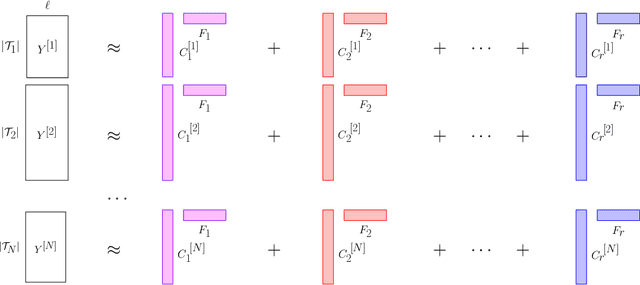
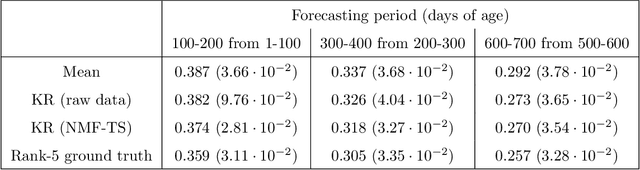
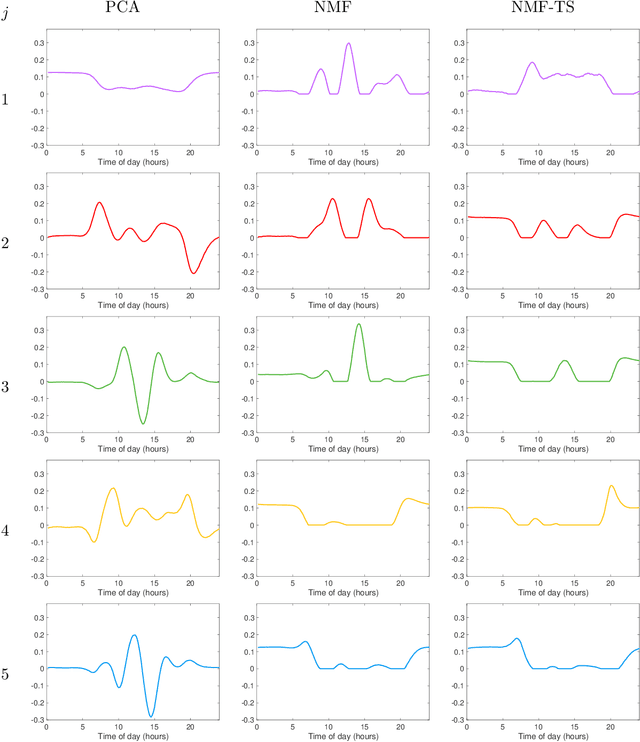
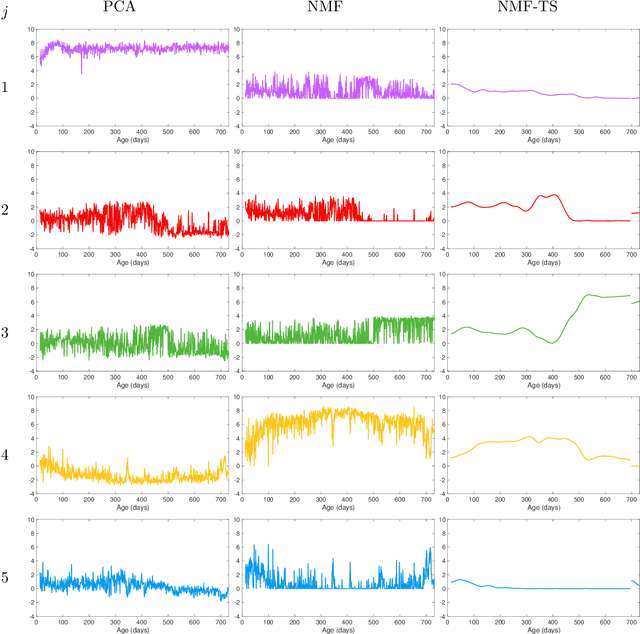
We propose a nonparametric model for time series with missing data based on low-rank matrix factorization. The model expresses each instance in a set of time series as a linear combination of a small number of shared basis functions. Constraining the functions and the corresponding coefficients to be nonnegative yields an interpretable low-dimensional representation of the data. A time-smoothing regularization term ensures that the model captures meaningful trends in the data, instead of overfitting short-term fluctuations. The low-dimensional representation makes it possible to detect outliers and cluster the time series according to the interpretable features extracted by the model, and also to perform forecasting via kernel regression. We apply our methodology to a large real-world dataset of infant-sleep data gathered by caregivers with a mobile-phone app. Our analysis automatically extracts daily-sleep patterns consistent with the existing literature. This allows us to compute sleep-development trends for the cohort, which characterize the emergence of circadian sleep and different napping habits. We apply our methodology to detect anomalous individuals, to cluster the cohort into groups with different sleeping tendencies, and to obtain improved predictions of future sleep behavior.

Prototypal Analysis and Prototypal Regression

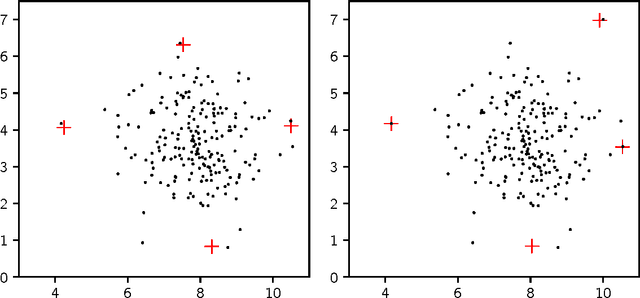
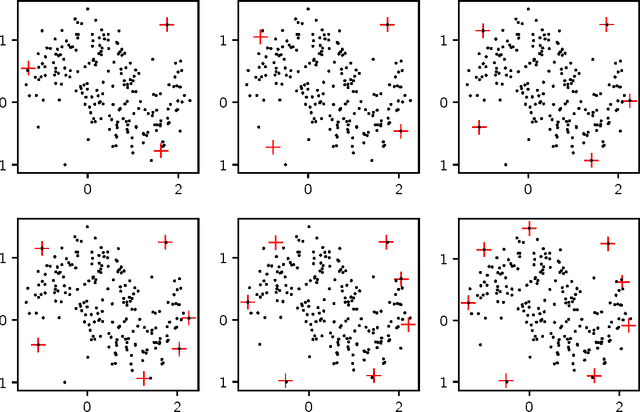
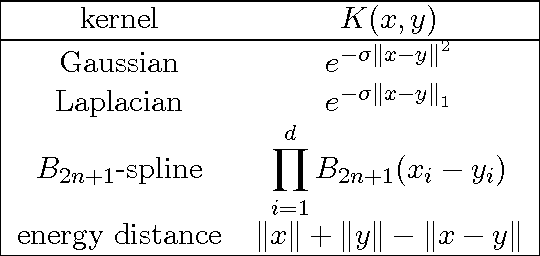
Prototypal analysis is introduced to overcome two shortcomings of archetypal analysis: its sensitivity to outliers and its non-locality, which reduces its applicability as a learning tool. Same as archetypal analysis, prototypal analysis finds prototypes through convex combination of the data points and approximates the data through convex combination of the archetypes, but it adds a penalty for using prototypes distant from the data points for their reconstruction. Prototypal analysis can be extended---via kernel embedding---to probability distributions, since the convexity of the prototypes makes them interpretable as mixtures. Finally, prototypal regression is developed, a robust supervised procedure which allows the use of distributions as either features or labels.