Adversarial Optimal Transport Through The Convolution Of Kernels With Evolving Measures
Paper and Code
Jun 09, 2020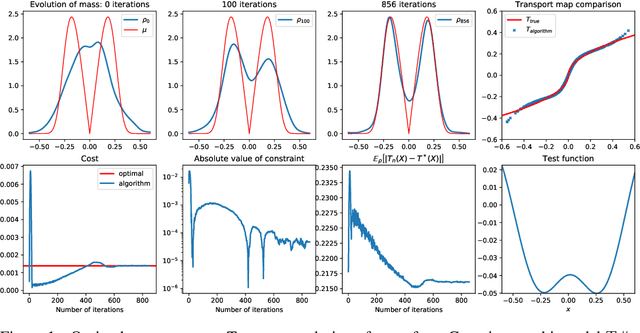


A novel algorithm is proposed to solve the sample-based optimal transport problem. An adversarial formulation of the push-forward condition uses a test function built as a convolution between an adaptive kernel and an evolving probability distribution $\nu$ over a latent variable $b$. Approximating this convolution by its simulation over evolving samples $b^i(t)$ of $\nu$, the parameterization of the test function reduces to determining the flow of these samples. This flow, discretized over discrete time steps $t_n$, is built from the composition of elementary maps. The optimal transport also follows a flow that, by duality, must follow the gradient of the test function. The representation of the test function as the Monte Carlo simulation of a distribution makes the algorithm robust to dimensionality, and its evolution under a memory-less flow produces rich, complex maps from simple parametric transformations. The algorithm is illustrated with numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge