Chenyue Wu
Prototypal Analysis and Prototypal Regression
Aug 23, 2017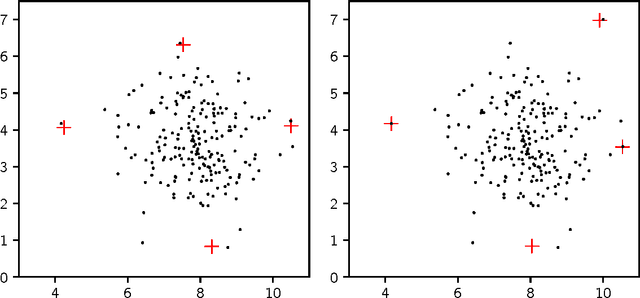

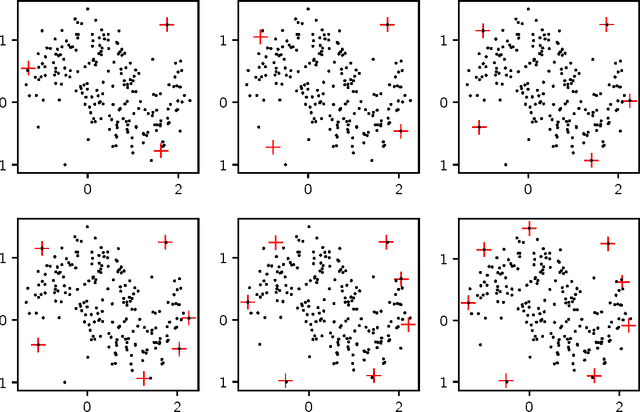
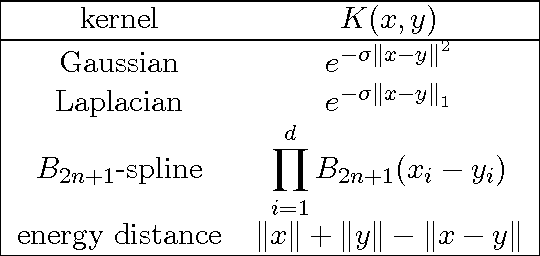
Abstract:Prototypal analysis is introduced to overcome two shortcomings of archetypal analysis: its sensitivity to outliers and its non-locality, which reduces its applicability as a learning tool. Same as archetypal analysis, prototypal analysis finds prototypes through convex combination of the data points and approximates the data through convex combination of the archetypes, but it adds a penalty for using prototypes distant from the data points for their reconstruction. Prototypal analysis can be extended---via kernel embedding---to probability distributions, since the convexity of the prototypes makes them interpretable as mixtures. Finally, prototypal regression is developed, a robust supervised procedure which allows the use of distributions as either features or labels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge