Zero-order Control Barrier Functions for Sampled-Data Systems with State and Input Dependent Safety Constraints

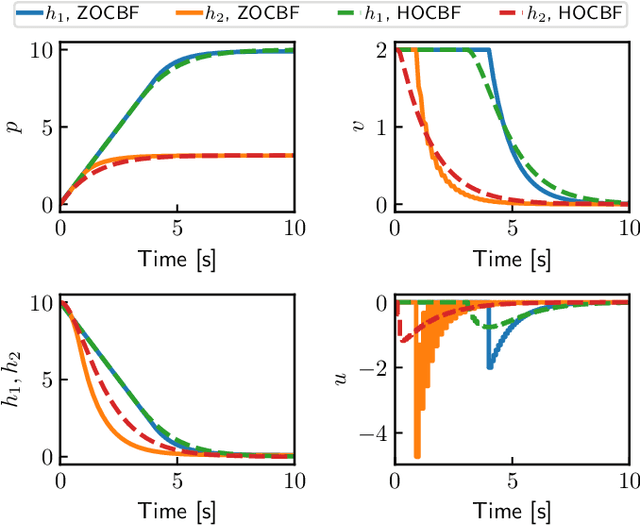
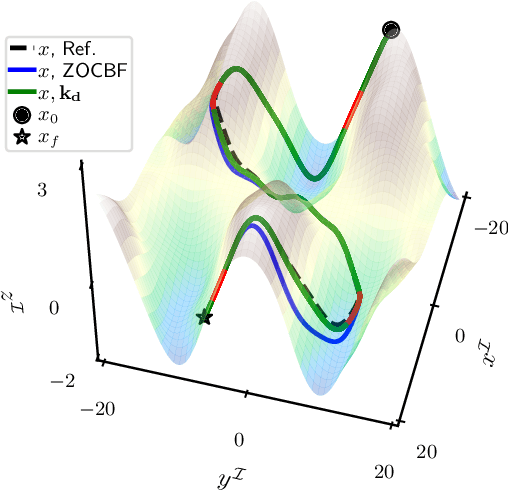
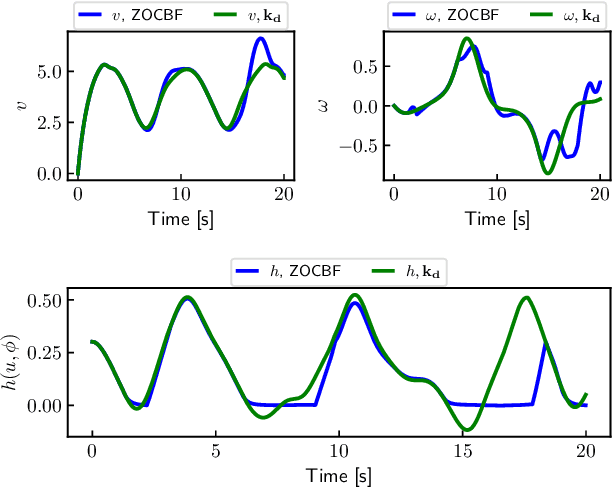
We propose a novel zero-order control barrier function (ZOCBF) for sampled-data systems to ensure system safety. Our formulation generalizes conventional control barrier functions and straightforwardly handles safety constraints with high-relative degrees or those that explicitly depend on both system states and inputs. The proposed ZOCBF condition does not require any differentiation operation. Instead, it involves computing the difference of the ZOCBF values at two consecutive sampling instants. We propose three numerical approaches to enforce the ZOCBF condition, tailored to different problem settings and available computational resources. We demonstrate the effectiveness of our approach through a collision avoidance example and a rollover prevention example on uneven terrains.

Rollover Prevention for Mobile Robots with Control Barrier Functions: Differentiator-Based Adaptation and Projection-to-State Safety

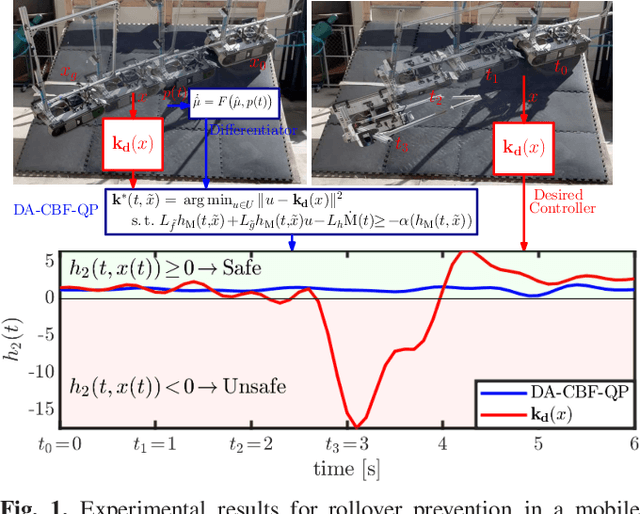
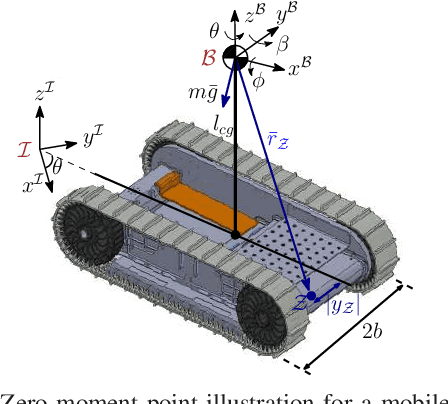
This paper develops rollover prevention guarantees for mobile robots using control barrier function (CBF) theory, and demonstrates these formal results experimentally. To this end, we consider a safety measure based on the zero moment point to provide conditions on the control input through the lens of CBFs. However, these conditions depend on time-varying and noisy parameters. To address this, we present a differentiator-based safety-critical controller that estimates these parameters and pairs Input-to-State Stable (ISS) differentiator dynamics with CBFs to achieve rigorous guarantees of safety. Additionally, to ensure safety in the presence of disturbance, we utilize a time-varying extension of Projection-to-State Safety (PSSf). The effectiveness of the proposed method is demonstrated through experiments on a tracked robot with a rollover potential on steep slopes.

Robust Control Barrier Functions using Uncertainty Estimation with Application to Mobile Robots

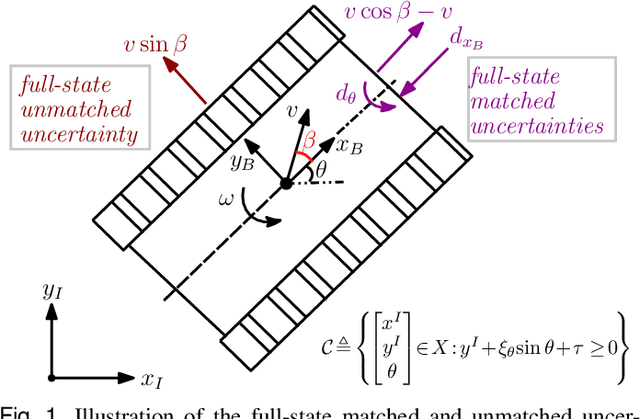
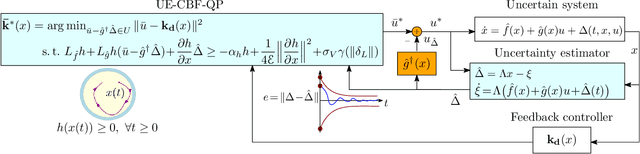
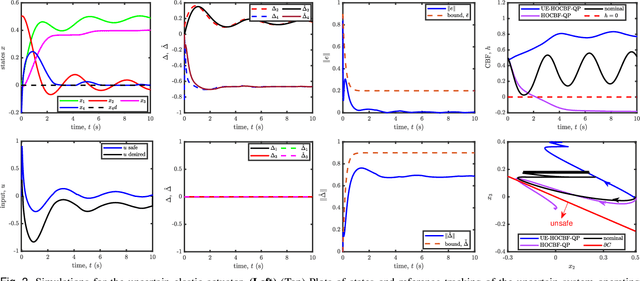
Model uncertainty poses a significant challenge to the implementation of safety-critical control systems. With this as motivation, this paper proposes a safe control design approach that guarantees the robustness of nonlinear feedback systems in the presence of matched or unmatched unmodelled system dynamics and external disturbances. Our approach couples control barrier functions (CBFs) with a new uncertainty/disturbance estimator to ensure robust safety against input and state-dependent model uncertainties. We prove upper bounds on the estimator's error and estimated outputs. We use an uncertainty estimator-based composite feedback control law to adaptively improve robust control performance under hard safety constraints by compensating for the matched uncertainty. Then, we robustify existing CBF constraints with this uncertainty estimate and the estimation error bounds to ensure robust safety via a quadratic program (CBF-QP). We also extend our method to higher-order CBFs (HOCBFs) to achieve safety under unmatched uncertainty, which causes relative degree differences with respect to control input and disturbance. We assume the relative degree difference is at most one, resulting in a second-order cone (SOC) condition. The proposed robust HOCBFs method is demonstrated in a simulation of an uncertain elastic actuator control problem. Finally, the efficacy of our method is experimentally demonstrated on a tracked robot with slope-induced matched and unmatched perturbations.