Taking advantage of a very simple property to efficiently infer NFAs

Grammatical inference consists in learning a formal grammar as a finite state machine or as a set of rewrite rules. In this paper, we are concerned with inferring Nondeterministic Finite Automata (NFA) that must accept some words, and reject some other words from a given sample. This problem can naturally be modeled in SAT. The standard model being enormous, some models based on prefixes, suffixes, and hybrids were designed to generate smaller SAT instances. There is a very simple and obvious property that says: if there is an NFA of size k for a given sample, there is also an NFA of size k+1. We first strengthen this property by adding some characteristics to the NFA of size k+1. Hence, we can use this property to tighten the bounds of the size of the minimal NFA for a given sample. We then propose simplified and refined models for NFA of size k+1 that are smaller than the initial models for NFA of size k. We also propose a reduction algorithm to build an NFA of size k from a specific NFA of size k+1. Finally, we validate our proposition with some experimentation that shows the efficiency of our approach.

Improved SAT models for NFA learning

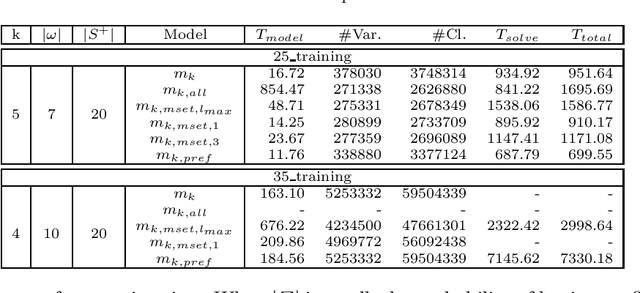
Grammatical inference is concerned with the study of algorithms for learning automata and grammars from words. We focus on learning Nondeterministic Finite Automaton of size k from samples of words. To this end, we formulate the problem as a SAT model. The generated SAT instances being enormous, we propose some model improvements, both in terms of the number of variables, the number of clauses, and clauses size. These improvements significantly reduce the instances, but at the cost of longer generation time. We thus try to balance instance size vs. generation and solving time. We also achieved some experimental comparisons and we analyzed our various model improvements.

GA and ILS for optimizing the size of NFA models

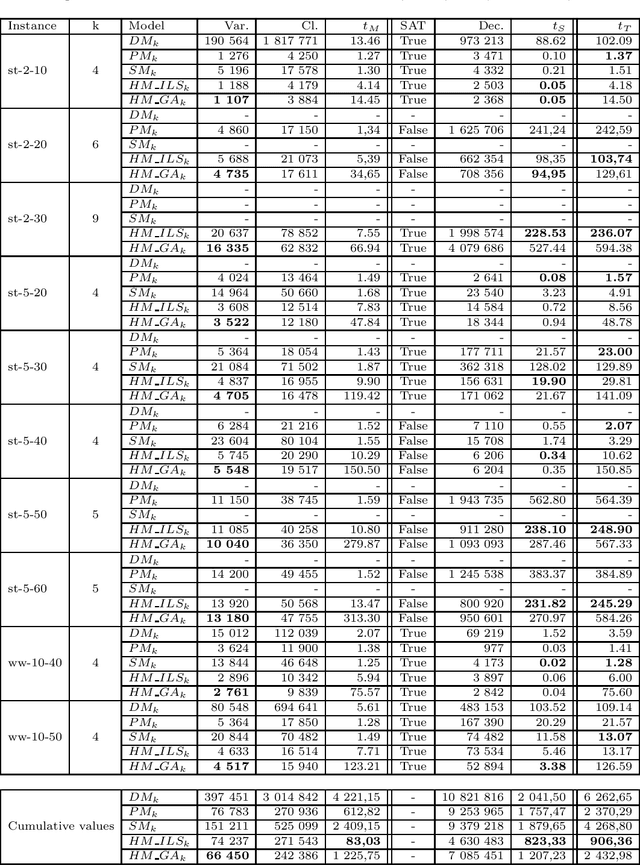
Grammatical inference consists in learning a formal grammar (as a set of rewrite rules or a finite state machine). We are concerned with learning Nondeterministic Finite Automata (NFA) of a given size from samples of positive and negative words. NFA can naturally be modeled in SAT. The standard model [1] being enormous, we also try a model based on prefixes [2] which generates smaller instances. We also propose a new model based on suffixes and a hybrid model based on prefixes and suffixes. We then focus on optimizing the size of generated SAT instances issued from the hybrid models. We present two techniques to optimize this combination, one based on Iterated Local Search (ILS), the second one based on Genetic Algorithm (GA). Optimizing the combination significantly reduces the SAT instances and their solving time, but at the cost of longer generation time. We, therefore, study the balance between generation time and solving time thanks to some experimental comparisons, and we analyze our various model improvements.

Set Constraint Model and Automated Encoding into SAT: Application to the Social Golfer Problem

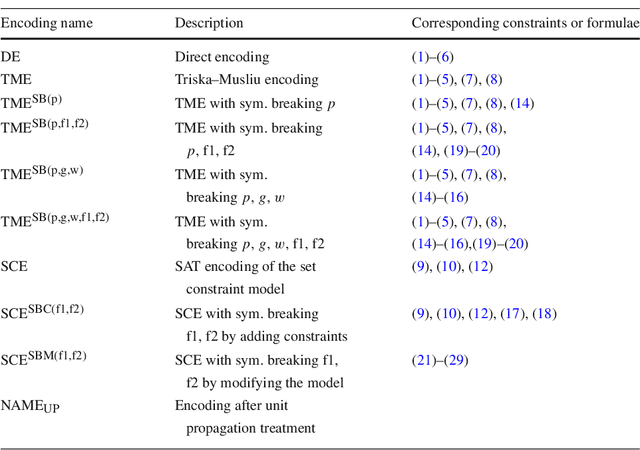
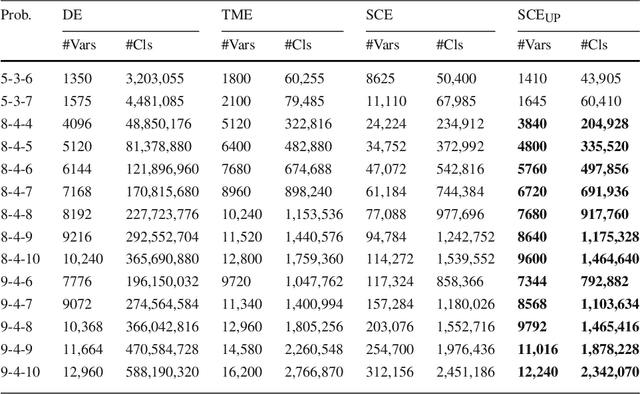
On the one hand, Constraint Satisfaction Problems allow one to declaratively model problems. On the other hand, propositional satisfiability problem (SAT) solvers can handle huge SAT instances. We thus present a technique to declaratively model set constraint problems and to encode them automatically into SAT instances. We apply our technique to the Social Golfer Problem and we also use it to break symmetries of the problem. Our technique is simpler, more declarative, and less error-prone than direct and improved hand modeling. The SAT instances that we automatically generate contain less clauses than improved hand-written instances such as in [20], and with unit propagation they also contain less variables. Moreover, they are well-suited for SAT solvers and they are solved faster as shown when solving difficult instances of the Social Golfer Problem.

Constraint-based analysis of composite solvers

Cooperative constraint solving is an area of constraint programming that studies the interaction between constraint solvers with the aim of discovering the interaction patterns that amplify the positive qualities of individual solvers. Automatisation and formalisation of such studies is an important issue of cooperative constraint solving. In this paper we present a constraint-based analysis of composite solvers that integrates reasoning about the individual solvers and the processed data. The idea is to approximate this reasoning by resolution of set constraints on the finite sets representing the predicates that express all the necessary properties. We illustrate application of our analysis to two important cooperation patterns: deterministic choice and loop.

Enhancing Constraint Propagation with Composition Operators

Constraint propagation is a general algorithmic approach for pruning the search space of a CSP. In a uniform way, K. R. Apt has defined a computation as an iteration of reduction functions over a domain. He has also demonstrated the need for integrating static properties of reduction functions (commutativity and semi-commutativity) to design specialized algorithms such as AC3 and DAC. We introduce here a set of operators for modeling compositions of reduction functions. Two of the major goals are to tackle parallel computations, and dynamic behaviours (such as slow convergence).

Constraint Programming viewed as Rule-based Programming

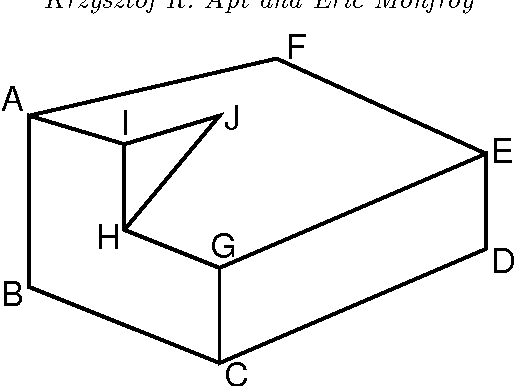
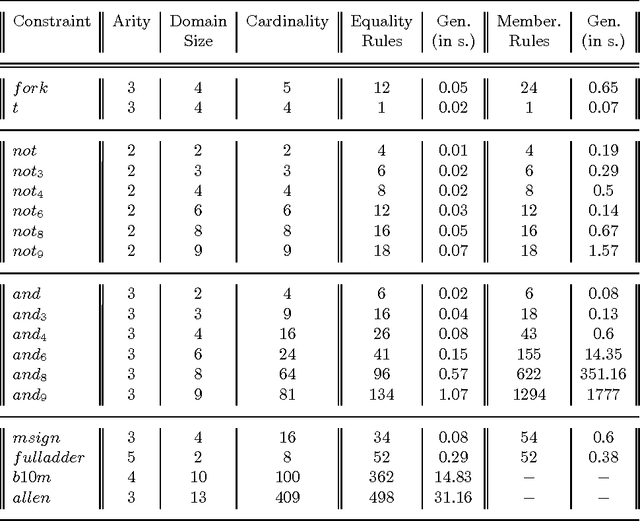
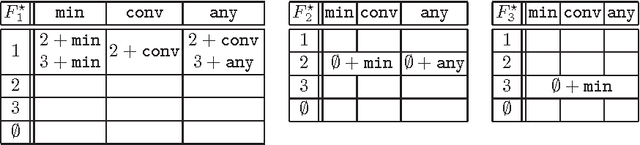
We study here a natural situation when constraint programming can be entirely reduced to rule-based programming. To this end we explain first how one can compute on constraint satisfaction problems using rules represented by simple first-order formulas. Then we consider constraint satisfaction problems that are based on predefined, explicitly given constraints. To solve them we first derive rules from these explicitly given constraints and limit the computation process to a repeated application of these rules, combined with labeling.We consider here two types of rules. The first type, that we call equality rules, leads to a new notion of local consistency, called {\em rule consistency} that turns out to be weaker than arc consistency for constraints of arbitrary arity (called hyper-arc consistency in \cite{MS98b}). For Boolean constraints rule consistency coincides with the closure under the well-known propagation rules for Boolean constraints. The second type of rules, that we call membership rules, yields a rule-based characterization of arc consistency. To show feasibility of this rule-based approach to constraint programming we show how both types of rules can be automatically generated, as {\tt CHR} rules of \cite{fruhwirth-constraint-95}. This yields an implementation of this approach to programming by means of constraint logic programming. We illustrate the usefulness of this approach to constraint programming by discussing various examples, including Boolean constraints, two typical examples of many valued logics, constraints dealing with Waltz's language for describing polyhedral scenes, and Allen's qualitative approach to temporal logic.

Automatic Generation of Constraint Propagation Algorithms for Small Finite Domains

We study here constraint satisfaction problems that are based on predefined, explicitly given finite constraints. To solve them we propose a notion of rule consistency that can be expressed in terms of rules derived from the explicit representation of the initial constraints. This notion of local consistency is weaker than arc consistency for constraints of arbitrary arity but coincides with it when all domains are unary or binary. For Boolean constraints rule consistency coincides with the closure under the well-known propagation rules for Boolean constraints. By generalizing the format of the rules we obtain a characterization of arc consistency in terms of so-called inclusion rules. The advantage of rule consistency and this rule based characterization of the arc consistency is that the algorithms that enforce both notions can be automatically generated, as CHR rules. So these algorithms could be integrated into constraint logic programming systems such as Eclipse. We illustrate the usefulness of this approach to constraint propagation by discussing the implementations of both algorithms and their use on various examples, including Boolean constraints, three valued logic of Kleene, constraints dealing with Waltz's language for describing polyhedreal scenes, and Allen's qualitative approach to temporal logic.