Constraint Programming viewed as Rule-based Programming

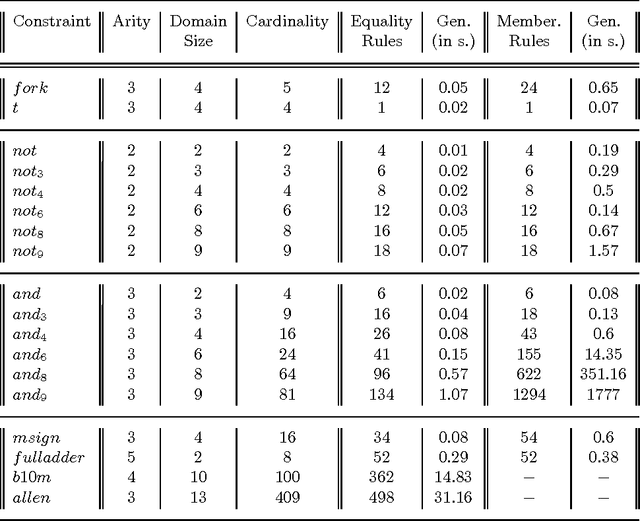
We study here a natural situation when constraint programming can be entirely reduced to rule-based programming. To this end we explain first how one can compute on constraint satisfaction problems using rules represented by simple first-order formulas. Then we consider constraint satisfaction problems that are based on predefined, explicitly given constraints. To solve them we first derive rules from these explicitly given constraints and limit the computation process to a repeated application of these rules, combined with labeling.We consider here two types of rules. The first type, that we call equality rules, leads to a new notion of local consistency, called {\em rule consistency} that turns out to be weaker than arc consistency for constraints of arbitrary arity (called hyper-arc consistency in \cite{MS98b}). For Boolean constraints rule consistency coincides with the closure under the well-known propagation rules for Boolean constraints. The second type of rules, that we call membership rules, yields a rule-based characterization of arc consistency. To show feasibility of this rule-based approach to constraint programming we show how both types of rules can be automatically generated, as {\tt CHR} rules of \cite{fruhwirth-constraint-95}. This yields an implementation of this approach to programming by means of constraint logic programming. We illustrate the usefulness of this approach to constraint programming by discussing various examples, including Boolean constraints, two typical examples of many valued logics, constraints dealing with Waltz's language for describing polyhedral scenes, and Allen's qualitative approach to temporal logic.