Using ATL to define advanced and flexible constraint model transformations

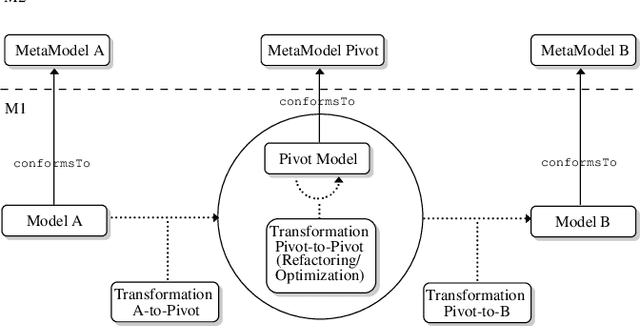
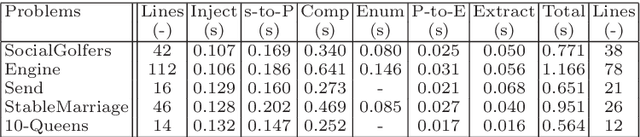
Transforming constraint models is an important task in re- cent constraint programming systems. User-understandable models are defined during the modeling phase but rewriting or tuning them is manda- tory to get solving-efficient models. We propose a new architecture al- lowing to define bridges between any (modeling or solver) languages and to implement model optimizations. This architecture follows a model- driven approach where the constraint modeling process is seen as a set of model transformations. Among others, an interesting feature is the def- inition of transformations as concept-oriented rules, i.e. based on types of model elements where the types are organized into a hierarchy called a metamodel.

Rewriting Constraint Models with Metamodels

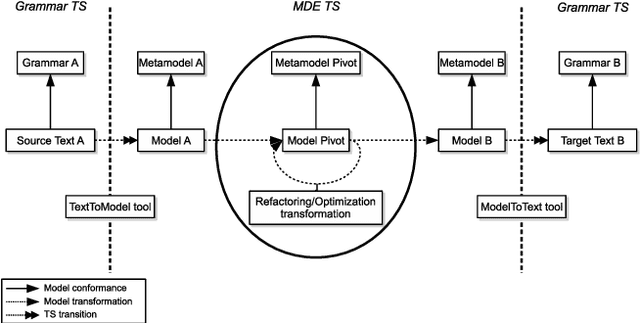
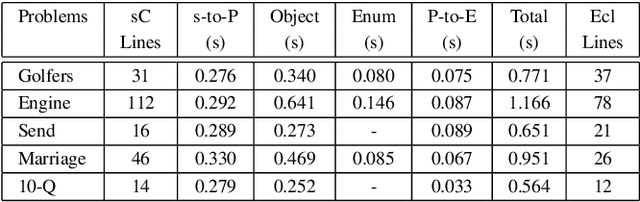
An important challenge in constraint programming is to rewrite constraint models into executable programs calculat- ing the solutions. This phase of constraint processing may require translations between constraint programming lan- guages, transformations of constraint representations, model optimizations, and tuning of solving strategies. In this paper, we introduce a pivot metamodel describing the common fea- tures of constraint models including different kinds of con- straints, statements like conditionals and loops, and other first-class elements like object classes and predicates. This metamodel is general enough to cope with the constructions of many languages, from object-oriented modeling languages to logic languages, but it is independent from them. The rewriting operations manipulate metamodel instances apart from languages. As a consequence, the rewriting operations apply whatever languages are selected and they are able to manage model semantic information. A bridge is created between the metamodel space and languages using parsing techniques. Tools from the software engineering world can be useful to implement this framework.

Model-Driven Constraint Programming

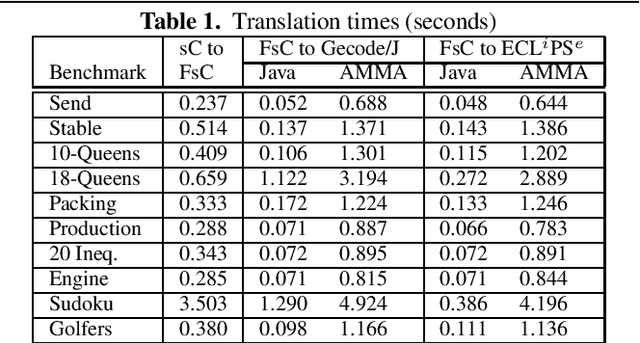
Constraint programming can definitely be seen as a model-driven paradigm. The users write programs for modeling problems. These programs are mapped to executable models to calculate the solutions. This paper focuses on efficient model management (definition and transformation). From this point of view, we propose to revisit the design of constraint-programming systems. A model-driven architecture is introduced to map solving-independent constraint models to solving-dependent decision models. Several important questions are examined, such as the need for a visual highlevel modeling language, and the quality of metamodeling techniques to implement the transformations. A main result is the s-COMMA platform that efficiently implements the chain from modeling to solving constraint problems

Directional Consistency for Continuous Numerical Constraints

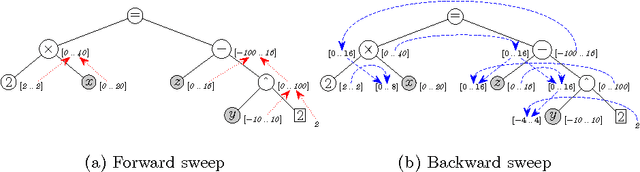
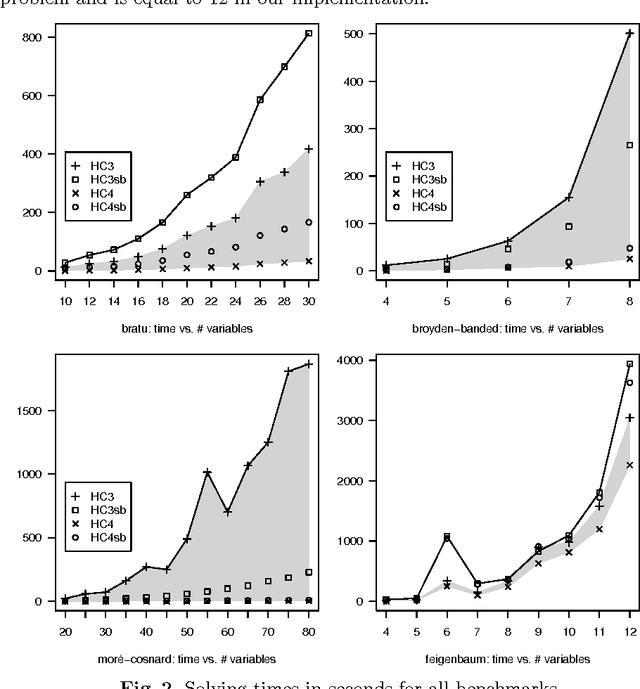
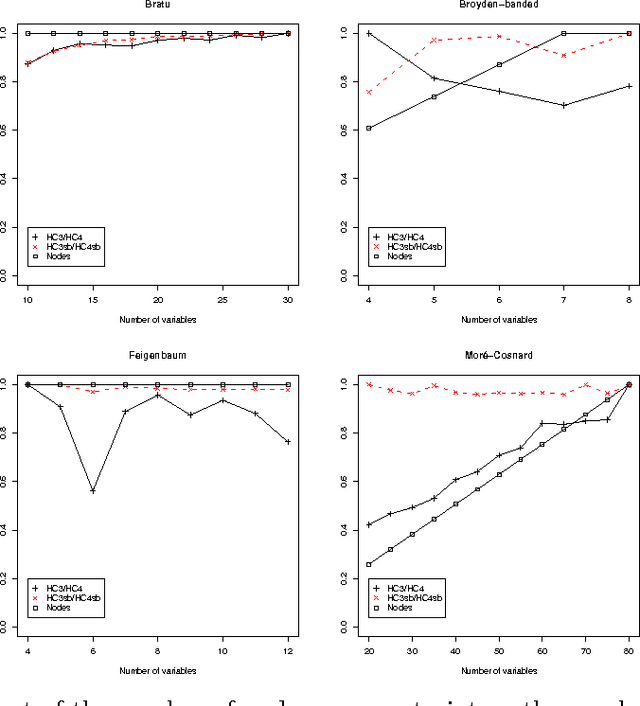
Bounds consistency is usually enforced on continuous constraints by first decomposing them into binary and ternary primitives. This decomposition has long been shown to drastically slow down the computation of solutions. To tackle this, Benhamou et al. have introduced an algorithm that avoids formally decomposing constraints. Its better efficiency compared to the former method has already been experimentally demonstrated. It is shown here that their algorithm implements a strategy to enforce on a continuous constraint a consistency akin to Directional Bounds Consistency as introduced by Dechter and Pearl for discrete problems. The algorithm is analyzed in this framework, and compared with algorithms that enforce bounds consistency. These theoretical results are eventually contrasted with new experimental results on standard benchmarks from the interval constraint community.

Enhancing Constraint Propagation with Composition Operators

Constraint propagation is a general algorithmic approach for pruning the search space of a CSP. In a uniform way, K. R. Apt has defined a computation as an iteration of reduction functions over a domain. He has also demonstrated the need for integrating static properties of reduction functions (commutativity and semi-commutativity) to design specialized algorithms such as AC3 and DAC. We introduce here a set of operators for modeling compositions of reduction functions. Two of the major goals are to tackle parallel computations, and dynamic behaviours (such as slow convergence).