Directional Consistency for Continuous Numerical Constraints

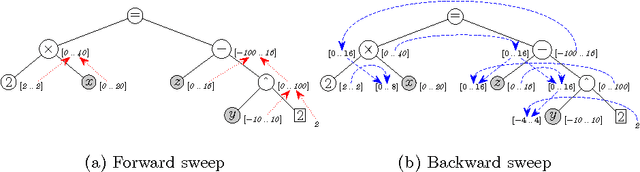
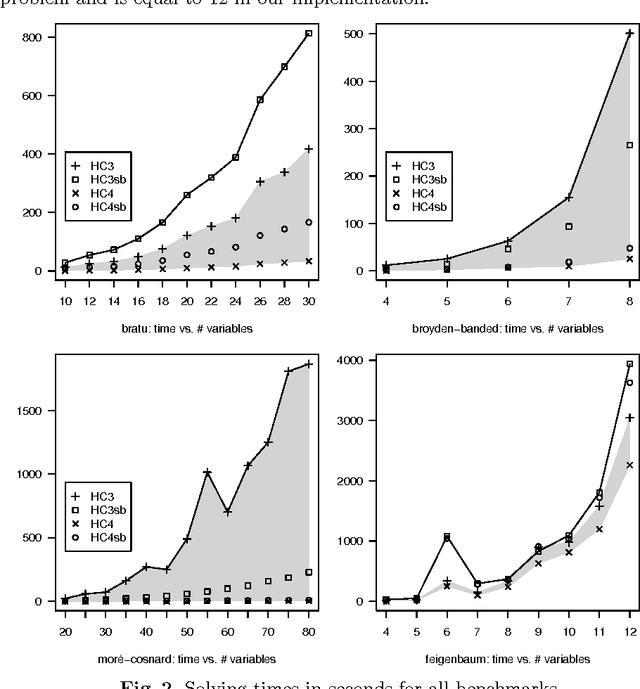
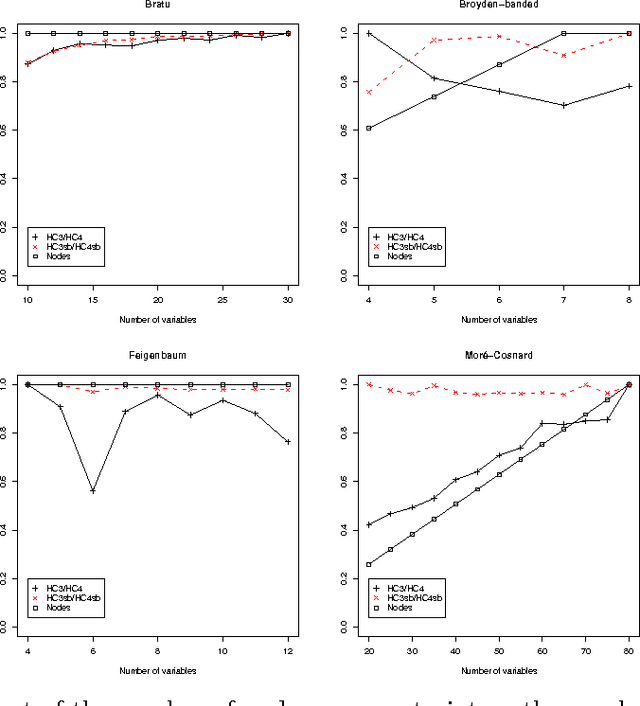
Bounds consistency is usually enforced on continuous constraints by first decomposing them into binary and ternary primitives. This decomposition has long been shown to drastically slow down the computation of solutions. To tackle this, Benhamou et al. have introduced an algorithm that avoids formally decomposing constraints. Its better efficiency compared to the former method has already been experimentally demonstrated. It is shown here that their algorithm implements a strategy to enforce on a continuous constraint a consistency akin to Directional Bounds Consistency as introduced by Dechter and Pearl for discrete problems. The algorithm is analyzed in this framework, and compared with algorithms that enforce bounds consistency. These theoretical results are eventually contrasted with new experimental results on standard benchmarks from the interval constraint community.

Interval Constraint Solving for Camera Control and Motion Planning

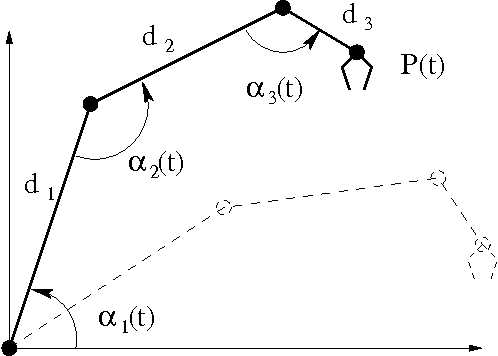
Many problems in robust control and motion planning can be reduced to either find a sound approximation of the solution space determined by a set of nonlinear inequalities, or to the ``guaranteed tuning problem'' as defined by Jaulin and Walter, which amounts to finding a value for some tuning parameter such that a set of inequalities be verified for all the possible values of some perturbation vector. A classical approach to solve these problems, which satisfies the strong soundness requirement, involves some quantifier elimination procedure such as Collins' Cylindrical Algebraic Decomposition symbolic method. Sound numerical methods using interval arithmetic and local consistency enforcement to prune the search space are presented in this paper as much faster alternatives for both soundly solving systems of nonlinear inequalities, and addressing the guaranteed tuning problem whenever the perturbation vector has dimension one. The use of these methods in camera control is investigated, and experiments with the prototype of a declarative modeller to express camera motion using a cinematic language are reported and commented.