Directional Consistency for Continuous Numerical Constraints
Paper and Code
Jun 16, 2004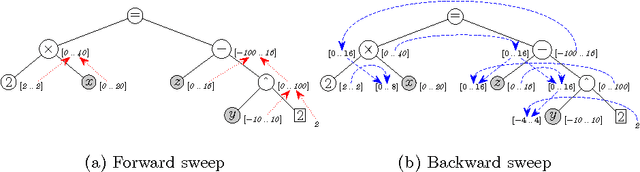
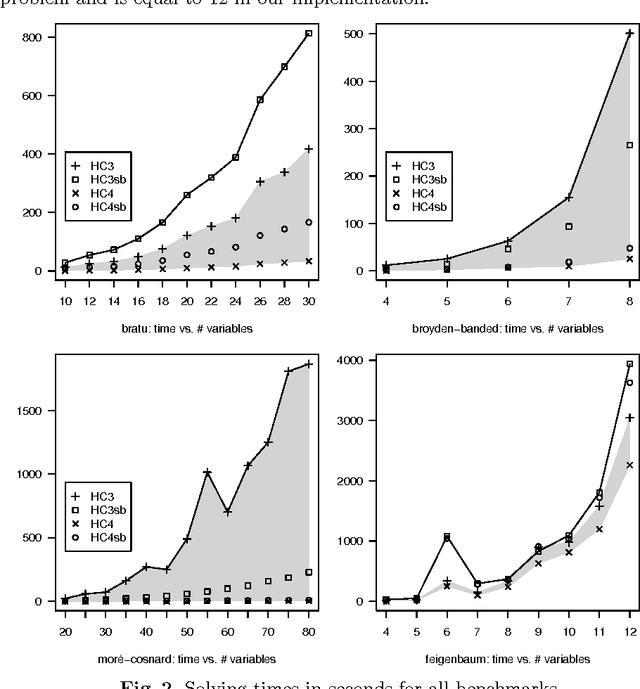
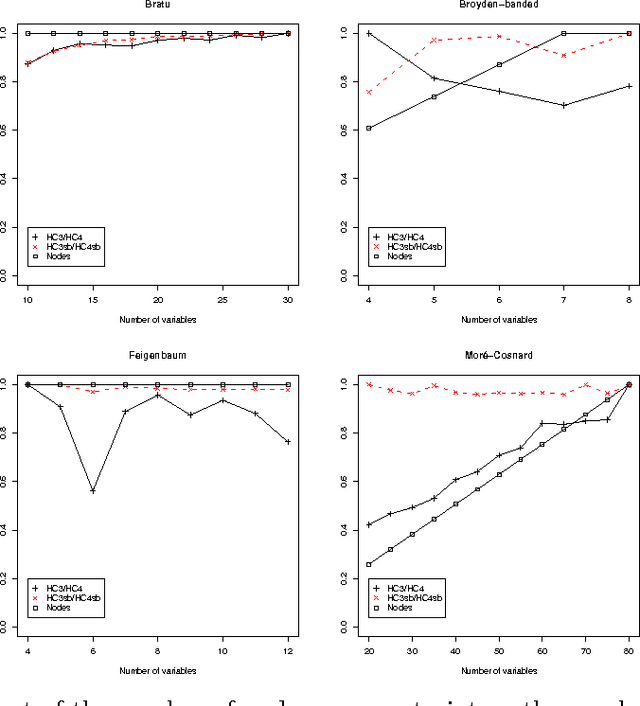
Bounds consistency is usually enforced on continuous constraints by first decomposing them into binary and ternary primitives. This decomposition has long been shown to drastically slow down the computation of solutions. To tackle this, Benhamou et al. have introduced an algorithm that avoids formally decomposing constraints. Its better efficiency compared to the former method has already been experimentally demonstrated. It is shown here that their algorithm implements a strategy to enforce on a continuous constraint a consistency akin to Directional Bounds Consistency as introduced by Dechter and Pearl for discrete problems. The algorithm is analyzed in this framework, and compared with algorithms that enforce bounds consistency. These theoretical results are eventually contrasted with new experimental results on standard benchmarks from the interval constraint community.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge