A Flexible Class of Dependence-aware Multi-Label Loss Functions

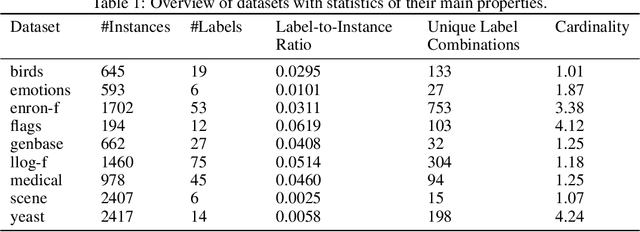
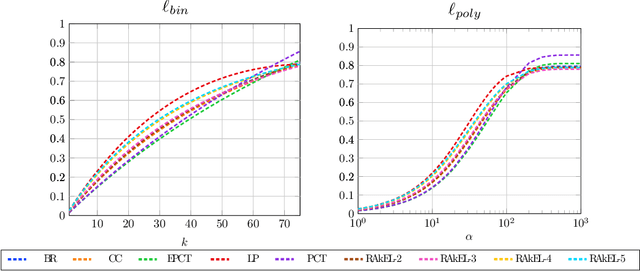
Multi-label classification is the task of assigning a subset of labels to a given query instance. For evaluating such predictions, the set of predicted labels needs to be compared to the ground-truth label set associated with that instance, and various loss functions have been proposed for this purpose. In addition to assessing predictive accuracy, a key concern in this regard is to foster and to analyze a learner's ability to capture label dependencies. In this paper, we introduce a new class of loss functions for multi-label classification, which overcome disadvantages of commonly used losses such as Hamming and subset 0/1. To this end, we leverage the mathematical framework of non-additive measures and integrals. Roughly speaking, a non-additive measure allows for modeling the importance of correct predictions of label subsets (instead of single labels), and thereby their impact on the overall evaluation, in a flexible way - by giving full importance to single labels and the entire label set, respectively, Hamming and subset 0/1 are rather extreme in this regard. We present concrete instantiations of this class, which comprise Hamming and subset 0/1 as special cases, and which appear to be especially appealing from a modeling perspective. The assessment of multi-label classifiers in terms of these losses is illustrated in an empirical study.

Conformal Rule-Based Multi-label Classification

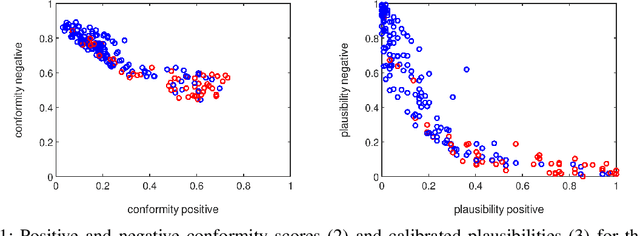
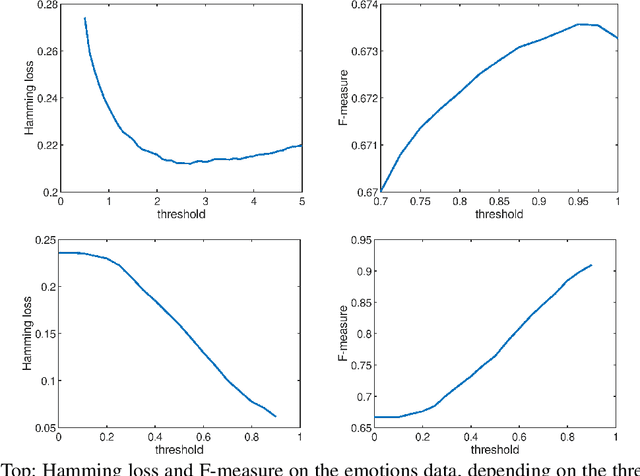
We advocate the use of conformal prediction (CP) to enhance rule-based multi-label classification (MLC). In particular, we highlight the mutual benefit of CP and rule learning: Rules have the ability to provide natural (non-)conformity scores, which are required by CP, while CP suggests a way to calibrate the assessment of candidate rules, thereby supporting better predictions and more elaborate decision making. We illustrate the potential usefulness of calibrated conformity scores in a case study on lazy multi-label rule learning.