Discrete Denoising Diffusion Approach to Integer Factorization

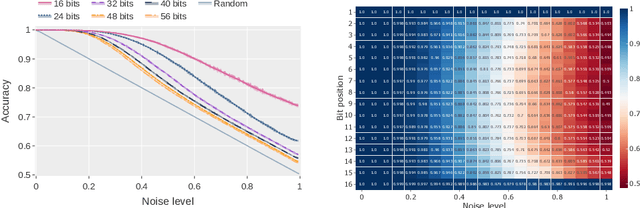
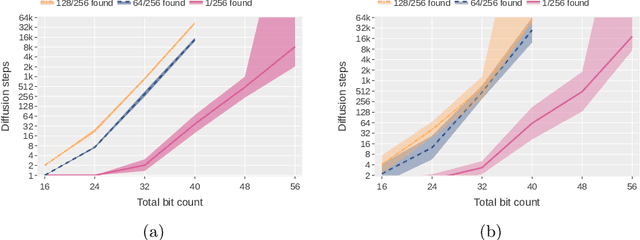
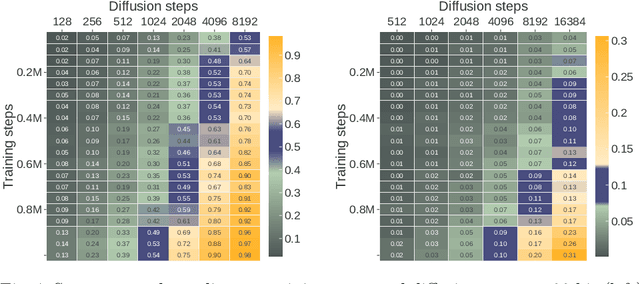
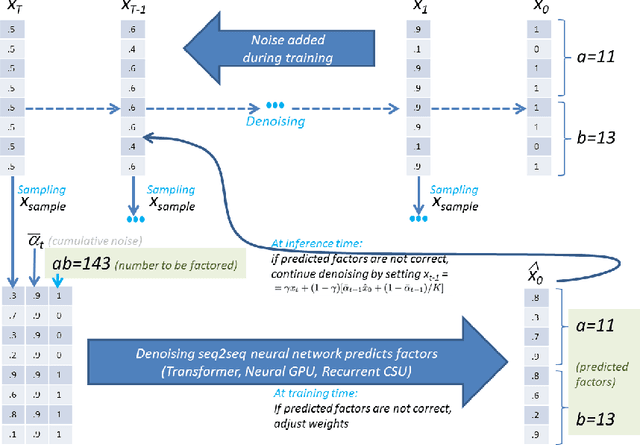
Integer factorization is a famous computational problem unknown whether being solvable in the polynomial time. With the rise of deep neural networks, it is interesting whether they can facilitate faster factorization. We present an approach to factorization utilizing deep neural networks and discrete denoising diffusion that works by iteratively correcting errors in a partially-correct solution. To this end, we develop a new seq2seq neural network architecture, employ relaxed categorical distribution and adapt the reverse diffusion process to cope better with inaccuracies in the denoising step. The approach is able to find factors for integers of up to 56 bits long. Our analysis indicates that investment in training leads to an exponential decrease of sampling steps required at inference to achieve a given success rate, thus counteracting an exponential run-time increase depending on the bit-length.

Gates are not what you need in RNNs

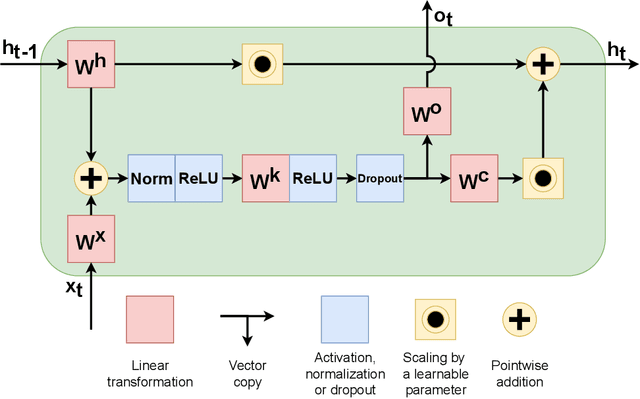
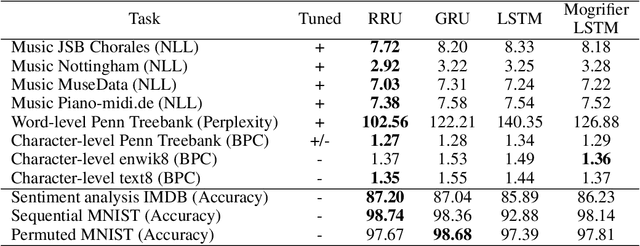
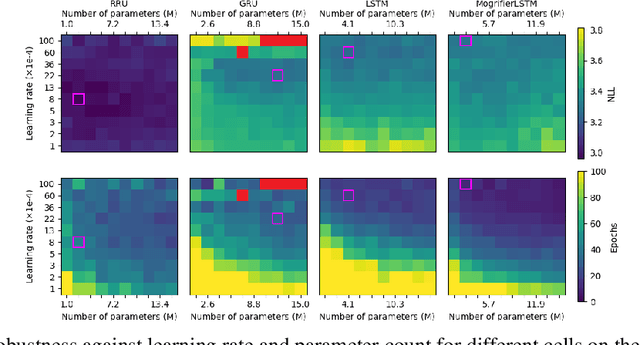
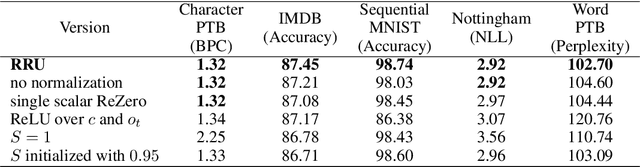
Recurrent neural networks have flourished in many areas. Consequently, we can see new RNN cells being developed continuously, usually by creating or using gates in a new, original way. But what if we told you that gates in RNNs are redundant? In this paper, we propose a new recurrent cell called Residual Recurrent Unit (RRU) which beats traditional cells and does not employ a single gate. It is based on the residual shortcut connection together with linear transformations, ReLU, and normalization. To evaluate our cell's effectiveness, we compare its performance against the widely-used GRU and LSTM cells and the recently proposed Mogrifier LSTM on several tasks including, polyphonic music modeling, language modeling, and sentiment analysis. Our experiments show that RRU outperforms the traditional gated units on most of these tasks. Also, it has better robustness to parameter selection, allowing immediate application in new tasks without much tuning. We have implemented the RRU in TensorFlow, and the code is made available at https://github.com/LUMII-Syslab/RRU .

Goal-Aware Neural SAT Solver

Modern neural networks obtain information about the problem and calculate the output solely from the input values. We argue that it is not always optimal, and the network's performance can be significantly improved by augmenting it with a query mechanism that allows the network to make several solution trials at run time and get feedback on the loss value on each trial. To demonstrate the capabilities of the query mechanism, we formulate an unsupervised (not dependant on labels) loss function for Boolean Satisfiability Problem (SAT) and theoretically show that it allows the network to extract rich information about the problem. We then propose a neural SAT solver with a query mechanism called QuerySAT and show that it outperforms the neural baseline on a wide range of SAT tasks and the classical baselines on SHA-1 preimage attack and 3-SAT task.