Sergejs Kozlovics
Denoising Diffusion for Sampling SAT Solutions
Nov 30, 2022
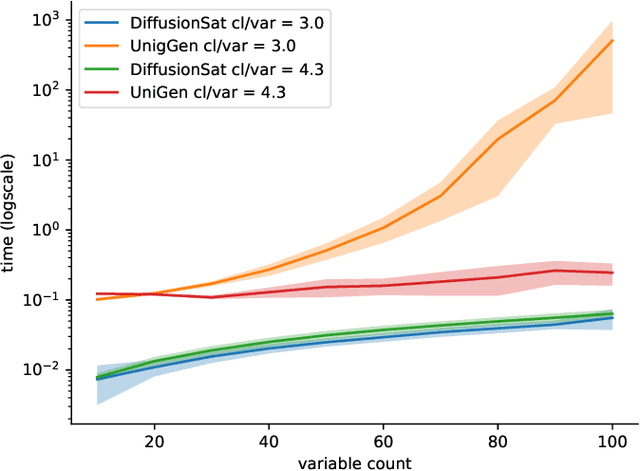
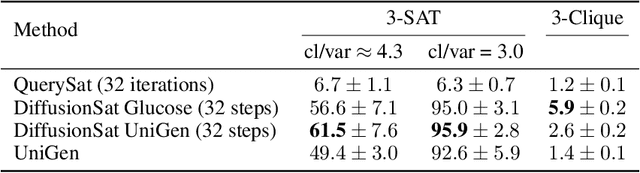

Abstract:Generating diverse solutions to the Boolean Satisfiability Problem (SAT) is a hard computational problem with practical applications for testing and functional verification of software and hardware designs. We explore the way to generate such solutions using Denoising Diffusion coupled with a Graph Neural Network to implement the denoising function. We find that the obtained accuracy is similar to the currently best purely neural method and the produced SAT solutions are highly diverse, even if the system is trained with non-random solutions from a standard solver.
Goal-Aware Neural SAT Solver
Jun 14, 2021Abstract:Modern neural networks obtain information about the problem and calculate the output solely from the input values. We argue that it is not always optimal, and the network's performance can be significantly improved by augmenting it with a query mechanism that allows the network to make several solution trials at run time and get feedback on the loss value on each trial. To demonstrate the capabilities of the query mechanism, we formulate an unsupervised (not dependant on labels) loss function for Boolean Satisfiability Problem (SAT) and theoretically show that it allows the network to extract rich information about the problem. We then propose a neural SAT solver with a query mechanism called QuerySAT and show that it outperforms the neural baseline on a wide range of SAT tasks and the classical baselines on SHA-1 preimage attack and 3-SAT task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge