Lower Bounds on the Worst-Case Complexity of Efficient Global Optimization

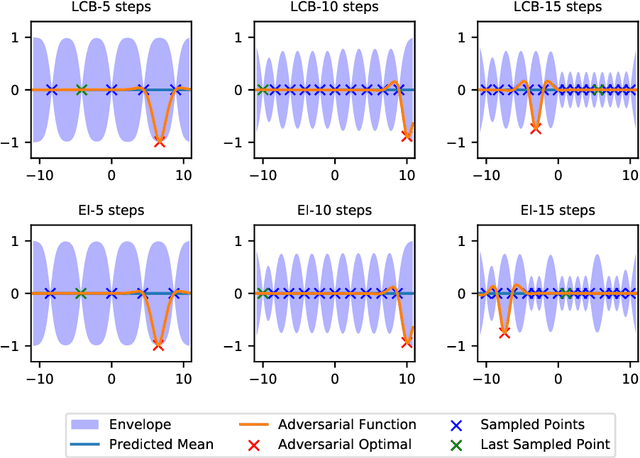
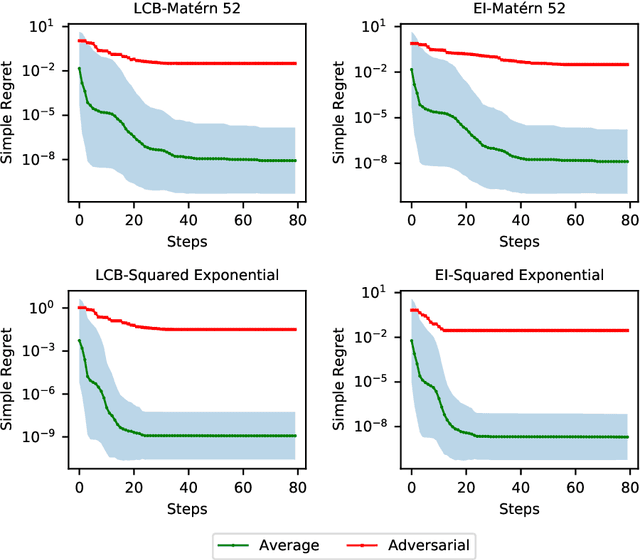
Efficient global optimization is a widely used method for optimizing expensive black-box functions such as tuning hyperparameter, and designing new material, etc. Despite its popularity, less attention has been paid to analyzing the inherent hardness of the problem although, given its extensive use, it is important to understand the fundamental limits of efficient global optimization algorithms. In this paper, we study the worst-case complexity of the efficient global optimization problem and, in contrast to existing kernel-specific results, we derive a unified lower bound for the complexity of efficient global optimization in terms of the metric entropy of a ball in its corresponding reproducing kernel Hilbert space~(RKHS). Specifically, we show that if there exists a deterministic algorithm that achieves suboptimality gap smaller than $\epsilon$ for any function $f\in S$ in $T$ function evaluations, it is necessary that $T$ is at least $\Omega\left(\frac{\log\mathcal{N}(S(\mathcal{X}), 4\epsilon,\|\cdot\|_\infty)}{\log(\frac{R}{\epsilon})}\right)$, where $\mathcal{N}(\cdot,\cdot,\cdot)$ is the covering number, $S$ is the ball centered at $0$ with radius $R$ in the RKHS and $S(\mathcal{X})$ is the restriction of $S$ over the feasible set $\mathcal{X}$. Moreover, we show that this lower bound nearly matches the upper bound attained by non-adaptive search algorithms for the commonly used squared exponential kernel and the Mat\'ern kernel with a large smoothness parameter $\nu$, up to a replacement of $d/2$ by $d$ and a logarithmic term $\log\frac{R}{\epsilon}$. That is to say, our lower bound is nearly optimal for these kernels.

Lessons Learned from Data-Driven Building Control Experiments: Contrasting Gaussian Process-based MPC, Bilevel DeePC, and Deep Reinforcement Learning

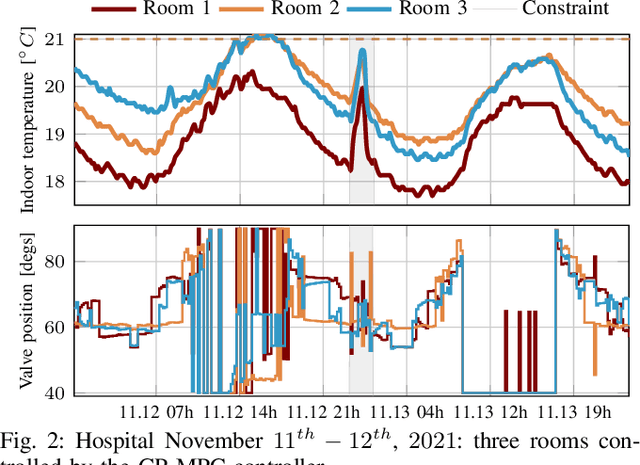
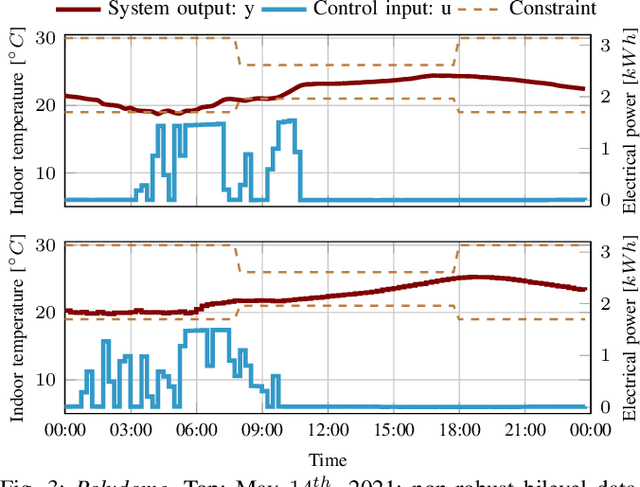
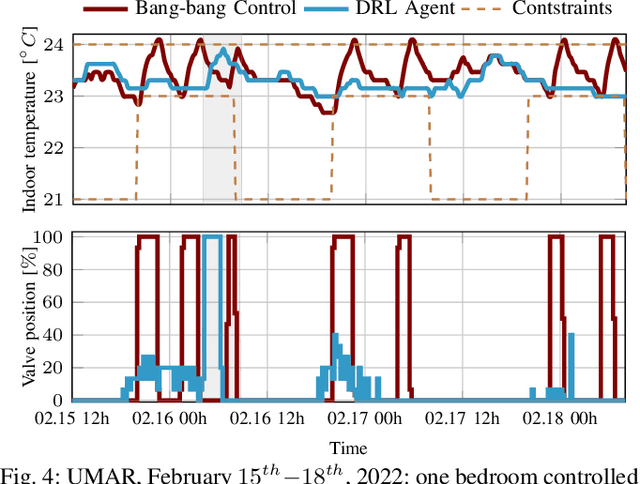
This manuscript offers the perspective of experimentalists on a number of modern data-driven techniques: model predictive control relying on Gaussian processes, adaptive data-driven control based on behavioral theory, and deep reinforcement learning. These techniques are compared in terms of data requirements, ease of use, computational burden, and robustness in the context of real-world applications. Our remarks and observations stem from a number of experimental investigations carried out in the field of building control in diverse environments, from lecture halls and apartment spaces to a hospital surgery center. The final goal is to support others in identifying what technique is best suited to tackle their own problems.

Robust Uncertainty Bounds in Reproducing Kernel Hilbert Spaces: A Convex Optimization Approach

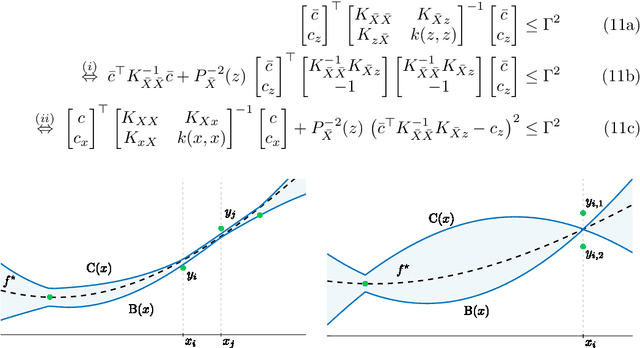
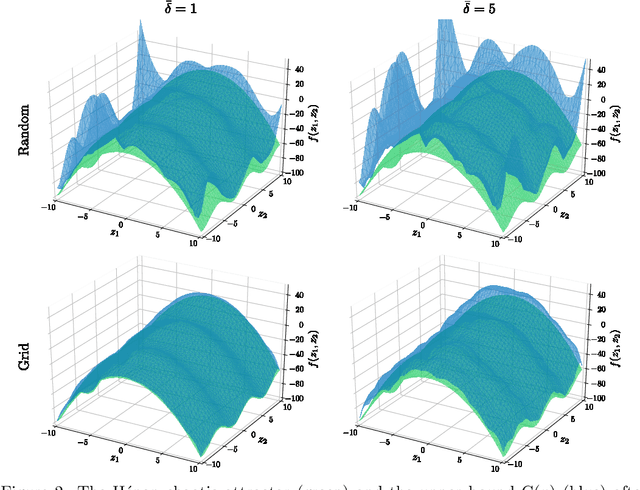
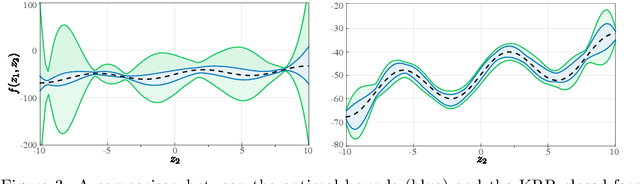
Let a labeled dataset be given with scattered samples and consider the hypothesis of the ground-truth belonging to the reproducing kernel Hilbert space (RKHS) of a known positive-definite kernel. It is known that out-of-sample bounds can be established at unseen input locations, thus limiting the risk associated with learning this function. We show how computing tight, finite-sample uncertainty bounds amounts to solving parametric quadratically constrained linear programs. In our setting, the outputs are assumed to be contaminated by bounded measurement noise that can otherwise originate from any compactly supported distribution. No independence assumptions are made on the available data. Numerical experiments are presented to compare the present results with other closed-form alternatives.

Deterministic error bounds for kernel-based learning techniques under bounded noise

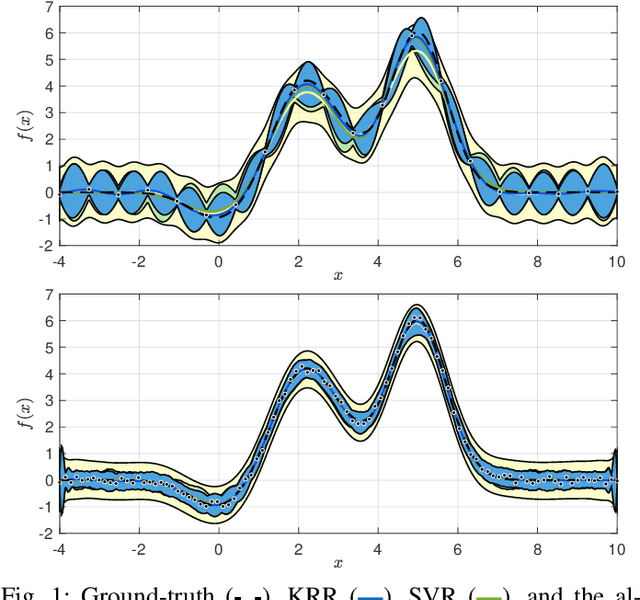
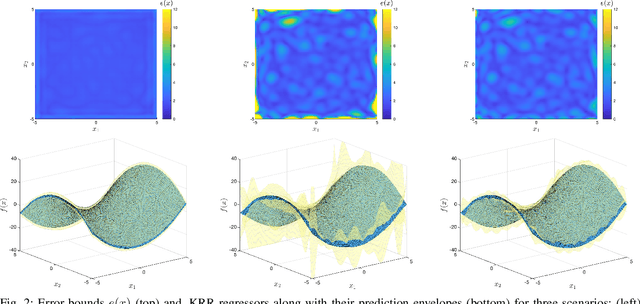
We consider the problem of reconstructing a function from a finite set of noise-corrupted samples. Two kernel algorithms are analyzed, namely kernel ridge regression and $\varepsilon$-support vector regression. By assuming the ground-truth function belongs to the reproducing kernel Hilbert space of the chosen kernel, and the measurement noise affecting the dataset is bounded, we adopt an approximation theory viewpoint to establish \textit{deterministic} error bounds for the two models. Finally, we discuss their connection with Gaussian processes and two numerical examples are provided. In establishing our inequalities, we hope to help bring the fields of non-parametric kernel learning and robust control closer to each other.