Robust Uncertainty Bounds in Reproducing Kernel Hilbert Spaces: A Convex Optimization Approach

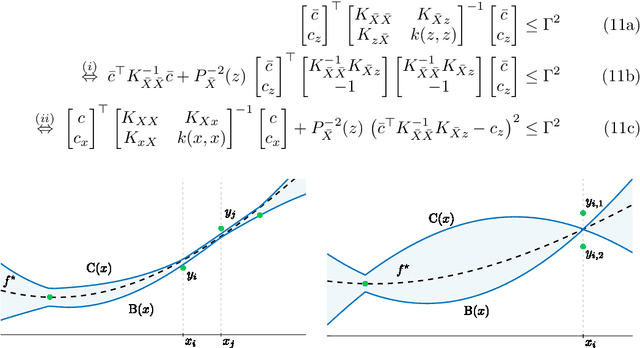
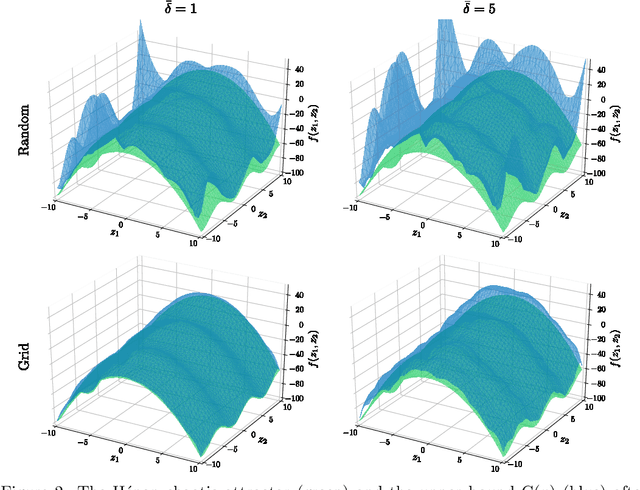
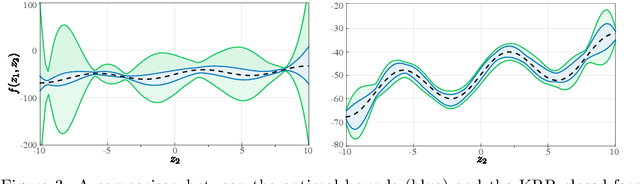
Let a labeled dataset be given with scattered samples and consider the hypothesis of the ground-truth belonging to the reproducing kernel Hilbert space (RKHS) of a known positive-definite kernel. It is known that out-of-sample bounds can be established at unseen input locations, thus limiting the risk associated with learning this function. We show how computing tight, finite-sample uncertainty bounds amounts to solving parametric quadratically constrained linear programs. In our setting, the outputs are assumed to be contaminated by bounded measurement noise that can otherwise originate from any compactly supported distribution. No independence assumptions are made on the available data. Numerical experiments are presented to compare the present results with other closed-form alternatives.

Deterministic error bounds for kernel-based learning techniques under bounded noise

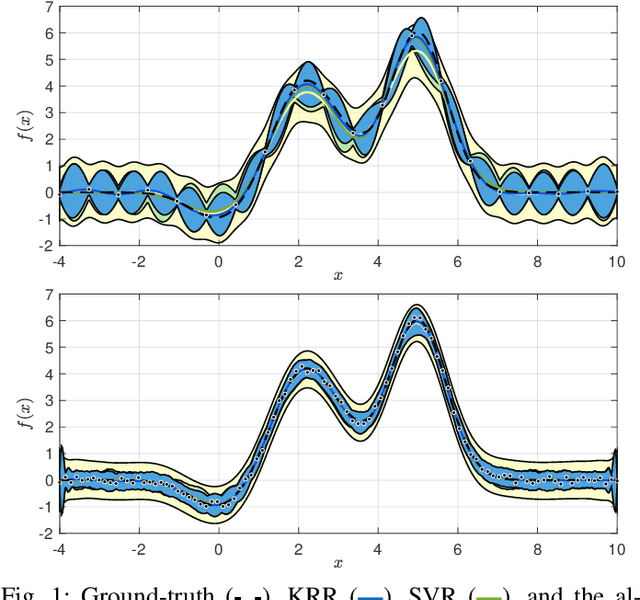
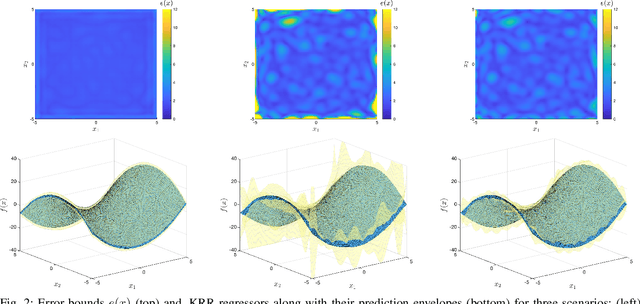
We consider the problem of reconstructing a function from a finite set of noise-corrupted samples. Two kernel algorithms are analyzed, namely kernel ridge regression and $\varepsilon$-support vector regression. By assuming the ground-truth function belongs to the reproducing kernel Hilbert space of the chosen kernel, and the measurement noise affecting the dataset is bounded, we adopt an approximation theory viewpoint to establish \textit{deterministic} error bounds for the two models. Finally, we discuss their connection with Gaussian processes and two numerical examples are provided. In establishing our inequalities, we hope to help bring the fields of non-parametric kernel learning and robust control closer to each other.