Adversarial Risk Bounds for Neural Networks through Sparsity based Compression

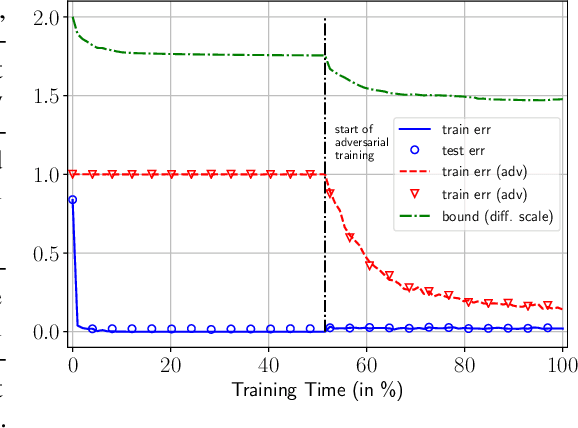
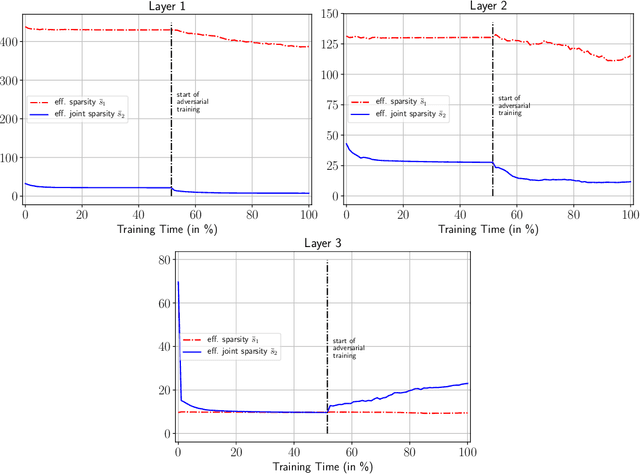
Neural networks have been shown to be vulnerable against minor adversarial perturbations of their inputs, especially for high dimensional data under $\ell_\infty$ attacks. To combat this problem, techniques like adversarial training have been employed to obtain models which are robust on the training set. However, the robustness of such models against adversarial perturbations may not generalize to unseen data. To study how robustness generalizes, recent works assume that the inputs have bounded $\ell_2$-norm in order to bound the adversarial risk for $\ell_\infty$ attacks with no explicit dimension dependence. In this work we focus on $\ell_\infty$ attacks on $\ell_\infty$ bounded inputs and prove margin-based bounds. Specifically, we use a compression based approach that relies on efficiently compressing the set of tunable parameters without distorting the adversarial risk. To achieve this, we apply the concept of effective sparsity and effective joint sparsity on the weight matrices of neural networks. This leads to bounds with no explicit dependence on the input dimension, neither on the number of classes. Our results show that neural networks with approximately sparse weight matrices not only enjoy enhanced robustness, but also better generalization.

On the Effect of Low-Rank Weights on Adversarial Robustness of Neural Networks

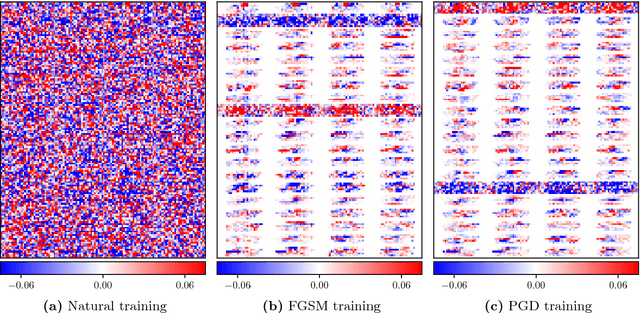
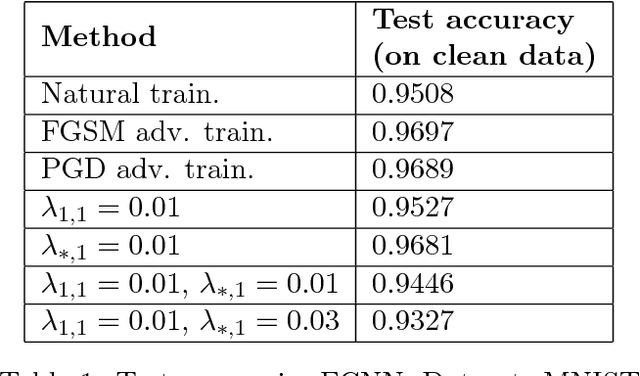
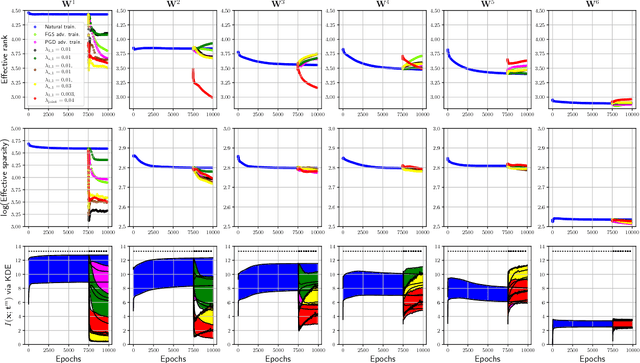
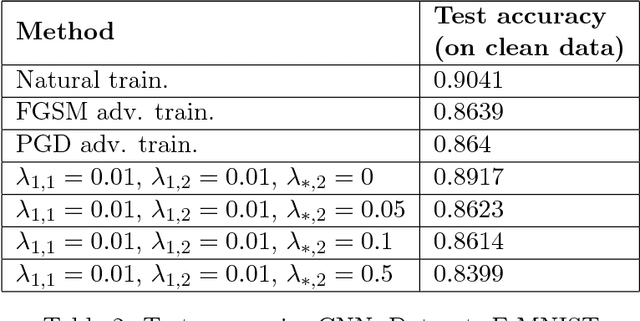
Recently, there has been an abundance of works on designing Deep Neural Networks (DNNs) that are robust to adversarial examples. In particular, a central question is which features of DNNs influence adversarial robustness and, therefore, can be to used to design robust DNNs. In this work, this problem is studied through the lens of compression which is captured by the low-rank structure of weight matrices. It is first shown that adversarial training tends to promote simultaneously low-rank and sparse structure in the weight matrices of neural networks. This is measured through the notions of effective rank and effective sparsity. In the reverse direction, when the low rank structure is promoted by nuclear norm regularization and combined with sparsity inducing regularizations, neural networks show significantly improved adversarial robustness. The effect of nuclear norm regularization on adversarial robustness is paramount when it is applied to convolutional neural networks. Although still not competing with adversarial training, this result contributes to understanding the key properties of robust classifiers.

Perturbation Analysis of Learning Algorithms: A Unifying Perspective on Generation of Adversarial Examples

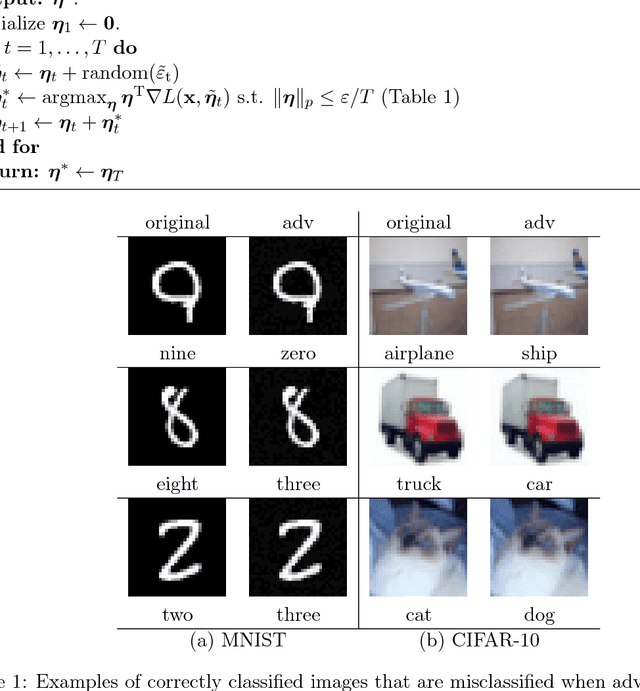
Despite the tremendous success of deep neural networks in various learning problems, it has been observed that adding an intentionally designed adversarial perturbation to inputs of these architectures leads to erroneous classification with high confidence in the prediction. In this work, we propose a general framework based on the perturbation analysis of learning algorithms which consists of convex programming and is able to recover many current adversarial attacks as special cases. The framework can be used to propose novel attacks against learning algorithms for classification and regression tasks under various new constraints with closed form solutions in many instances. In particular we derive new attacks against classification algorithms which are shown to achieve comparable performances to notable existing attacks. The framework is then used to generate adversarial perturbations for regression tasks which include single pixel and single subset attacks. By applying this method to autoencoding and image colorization tasks, it is shown that adversarial perturbations can effectively perturb the output of regression tasks as well.

On Generation of Adversarial Examples using Convex Programming

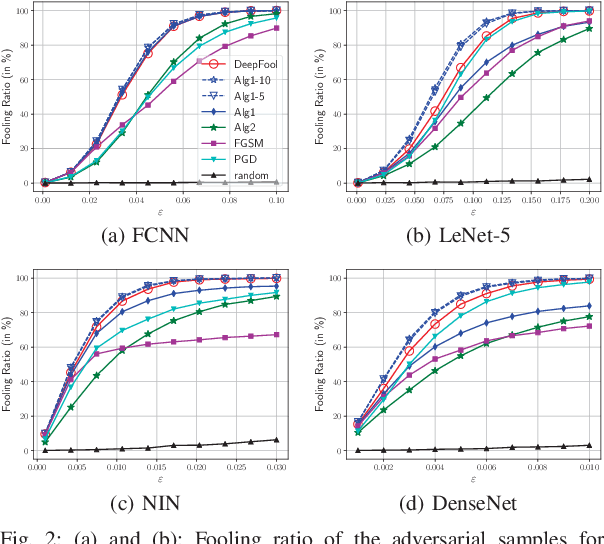
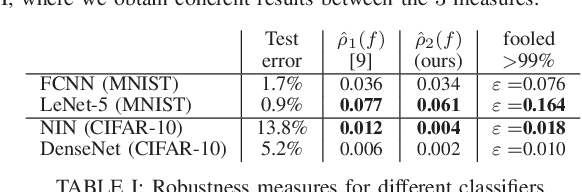
It has been observed that deep learning architectures tend to make erroneous decisions with high reliability for particularly designed adversarial instances. In this work, we show that the perturbation analysis of these architectures provides a framework for generating adversarial instances by convex programming which, for classification tasks, is able to recover variants of existing non-adaptive adversarial methods. The proposed framework can be used for the design of adversarial noise under various desirable constraints and different types of networks. Moreover, this framework is capable of explaining various existing adversarial methods and can be used to derive new algorithms as well. Furthermore, we make use of these results to obtain novel algorithms. Experiments show the competitive performance of the obtained solutions, in terms of fooling ratio, when benchmarked with well-known adversarial methods.