Outlyingness Scores with Cluster Catch Digraphs

This paper introduces two novel, outlyingness scores (OSs) based on Cluster Catch Digraphs (CCDs): Outbound Outlyingness Score (OOS) and Inbound Outlyingness Score (IOS). These scores enhance the interpretability of outlier detection results. Both OSs employ graph-, density-, and distribution-based techniques, tailored to high-dimensional data with varying cluster shapes and intensities. OOS evaluates the outlyingness of a point relative to its nearest neighbors, while IOS assesses the total ``influence" a point receives from others within its cluster. Both OSs effectively identify global and local outliers, invariant to data collinearity. Moreover, IOS is robust to the masking problems. With extensive Monte Carlo simulations, we compare the performance of both OSs with CCD-based, traditional, and state-of-the-art outlier detection methods. Both OSs exhibit substantial overall improvements over the CCD-based methods in both artificial and real-world data sets, particularly with IOS, which delivers the best overall performance among all the methods, especially in high-dimensional settings. Keywords: Outlier detection, Outlyingness score, Graph-based clustering, Cluster catch digraphs, High-dimensional data.

Cluster Catch Digraphs with the Nearest Neighbor Distance

We introduce a new method for clustering based on Cluster Catch Digraphs (CCDs). The new method addresses the limitations of RK-CCDs by employing a new variant of spatial randomness test that employs the nearest neighbor distance (NND) instead of the Ripley's K function used by RK-CCDs. We conduct a comprehensive Monte Carlo analysis to assess the performance of our method, considering factors such as dimensionality, data set size, number of clusters, cluster volumes, and inter-cluster distance. Our method is particularly effective for high-dimensional data sets, comparable to or outperforming KS-CCDs and RK-CCDs that rely on a KS-type statistic or the Ripley's K function. We also evaluate our methods using real and complex data sets, comparing them to well-known clustering methods. Again, our methods exhibit competitive performance, producing high-quality clusters with desirable properties. Keywords: Graph-based clustering, Cluster catch digraphs, High-dimensional data, The nearest neighbor distance, Spatial randomness test

Outlier Detection with Cluster Catch Digraphs

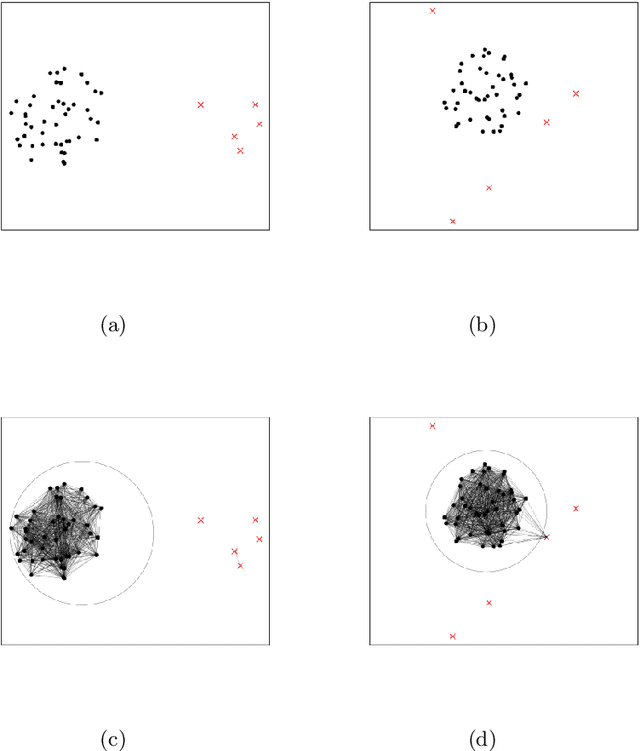
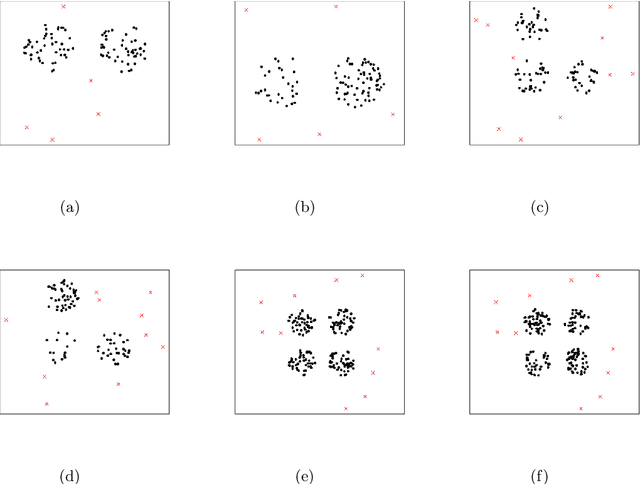
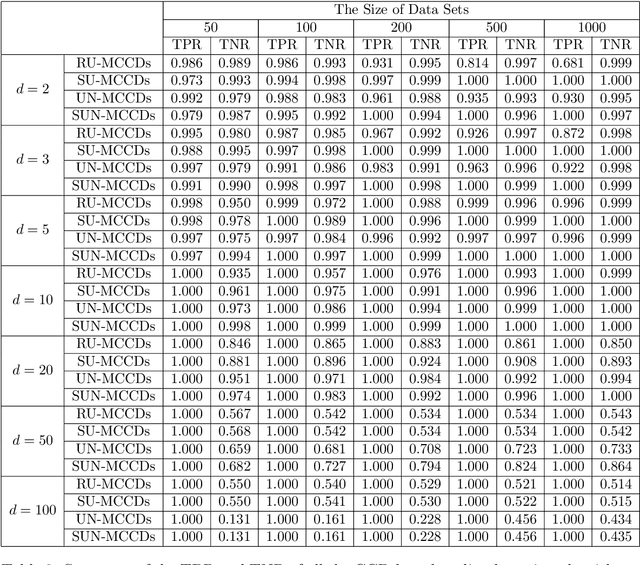
This paper introduces a novel family of outlier detection algorithms based on Cluster Catch Digraphs (CCDs), specifically tailored to address the challenges of high dimensionality and varying cluster shapes, which deteriorate the performance of most traditional outlier detection methods. We propose the Uniformity-Based CCD with Mutual Catch Graph (U-MCCD), the Uniformity- and Neighbor-Based CCD with Mutual Catch Graph (UN-MCCD), and their shape-adaptive variants (SU-MCCD and SUN-MCCD), which are designed to detect outliers in data sets with arbitrary cluster shapes and high dimensions. We present the advantages and shortcomings of these algorithms and provide the motivation or need to define each particular algorithm. Through comprehensive Monte Carlo simulations, we assess their performance and demonstrate the robustness and effectiveness of our algorithms across various settings and contamination levels. We also illustrate the use of our algorithms on various real-life data sets. The U-MCCD algorithm efficiently identifies outliers while maintaining high true negative rates, and the SU-MCCD algorithm shows substantial improvement in handling non-uniform clusters. Additionally, the UN-MCCD and SUN-MCCD algorithms address the limitations of existing methods in high-dimensional spaces by utilizing Nearest Neighbor Distances (NND) for clustering and outlier detection. Our results indicate that these novel algorithms offer substantial advancements in the accuracy and adaptability of outlier detection, providing a valuable tool for various real-world applications. Keyword: Outlier detection, Graph-based clustering, Cluster catch digraphs, $k$-nearest-neighborhood, Mutual catch graphs, Nearest neighbor distance.

Parameter Free Clustering with Cluster Catch Digraphs (Technical Report)

We propose clustering algorithms based on a recently developed geometric digraph family called cluster catch digraphs (CCDs). These digraphs are used to devise clustering methods that are hybrids of density-based and graph-based clustering methods. CCDs are appealing digraphs for clustering, since they estimate the number of clusters; however, CCDs (and density-based methods in general) require some information on a parameter representing the \emph{intensity} of assumed clusters in the data set. We propose algorithms that are parameter free versions of the CCD algorithm and does not require a specification of the intensity parameter whose choice is often critical in finding an optimal partitioning of the data set. We estimate the number of convex clusters by borrowing a tool from spatial data analysis, namely Ripley's $K$ function. We call our new digraphs utilizing the $K$ function as RK-CCDs. We show that the minimum dominating sets of RK-CCDs estimate and distinguish the clusters from noise clusters in a data set, and hence allow the estimation of the correct number of clusters. Our robust clustering algorithms are comprised of methods that estimate both the number of clusters and the intensity parameter, making them completely parameter free. We conduct Monte Carlo simulations and use real life data sets to compare RK-CCDs with some commonly used density-based and prototype-based clustering methods.

Classification of Imbalanced Data with a Geometric Digraph Family

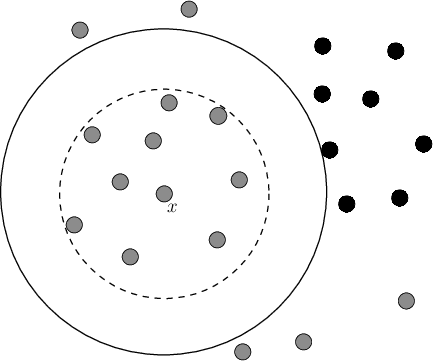
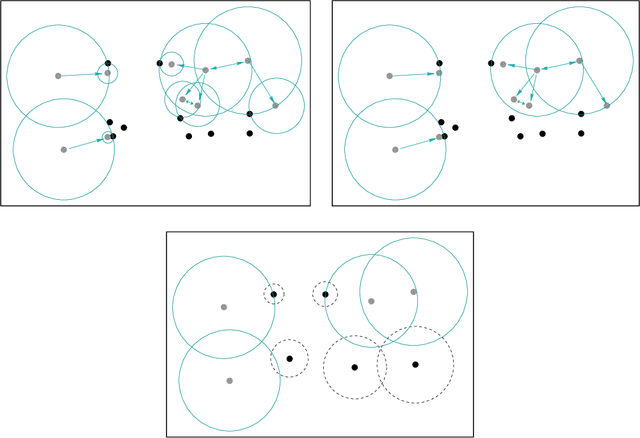
We use a geometric digraph family called class cover catch digraphs (CCCDs) to tackle the class imbalance problem in statistical classification. CCCDs provide graph theoretic solutions to the class cover problem and have been employed in classification. We assess the classification performance of CCCD classifiers by extensive Monte Carlo simulations, comparing them with other classifiers commonly used in the literature. In particular, we show that CCCD classifiers perform relatively well when one class is more frequent than the other in a two-class setting, an example of the class imbalance problem. We also point out the relationship between class imbalance and class overlapping problems, and their influence on the performance of CCCD classifiers and other classification methods as well as some state-of-the-art algorithms which are robust to class imbalance by construction. Experiments on both simulated and real data sets indicate that CCCD classifiers are robust to the class imbalance problem. CCCDs substantially undersample from the majority class while preserving the information on the discarded points during the undersampling process. Many state-of-the-art methods, however, keep this information by means of ensemble classifiers, but CCCDs yield only a single classifier with the same property, making it both appealing and fast.

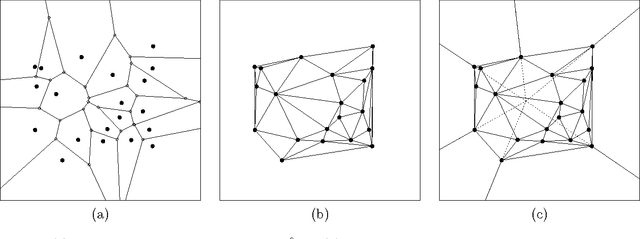
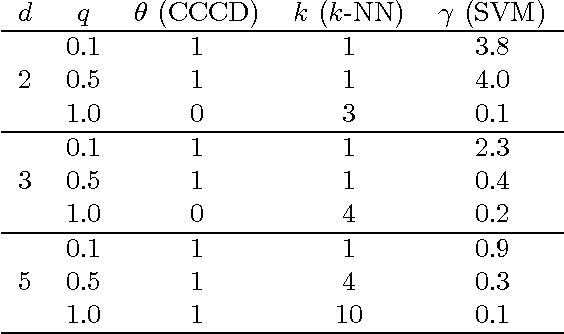
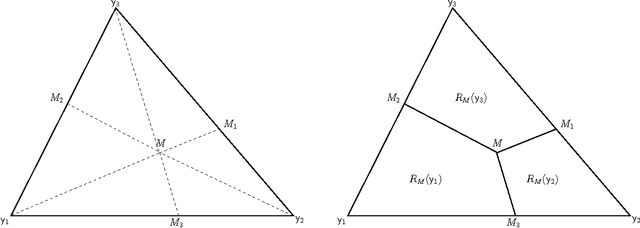
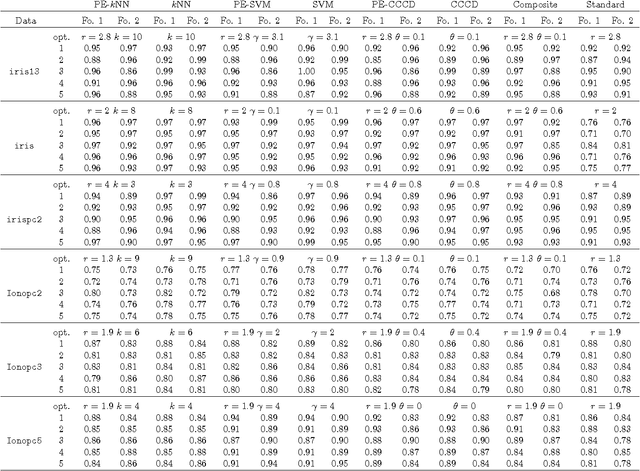
Classification Using Proximity Catch Digraphs (Technical Report)

We employ random geometric digraphs to construct semi-parametric classifiers. These data-random digraphs are from parametrized random digraph families called proximity catch digraphs (PCDs). A related geometric digraph family, class cover catch digraph (CCCD), has been used to solve the class cover problem by using its approximate minimum dominating set. CCCDs showed relatively good performance in the classification of imbalanced data sets, and although CCCDs have a convenient construction in $\mathbb{R}^d$, finding minimum dominating sets is NP-hard and its probabilistic behaviour is not mathematically tractable except for $d=1$. On the other hand, a particular family of PCDs, called \emph{proportional-edge} PCDs (PE-PCDs), has mathematical tractable minimum dominating sets in $\mathbb{R}^d$; however their construction in higher dimensions may be computationally demanding. More specifically, we show that the classifiers based on PE-PCDs are prototype-based classifiers such that the exact minimum number of prototypes (equivalent to minimum dominating sets) are found in polynomial time on the number of observations. We construct two types of classifiers based on PE-PCDs. One is a family of hybrid classifiers depend on the location of the points of the training data set, and another type is a family of classifiers solely based on class covers. We assess the classification performance of our PE-PCD based classifiers by extensive Monte Carlo simulations, and compare them with that of other commonly used classifiers. We also show that, similar to CCCD classifiers, our classifiers are relatively better in classification in the presence of class imbalance.