Outlyingness Scores with Cluster Catch Digraphs

This paper introduces two novel, outlyingness scores (OSs) based on Cluster Catch Digraphs (CCDs): Outbound Outlyingness Score (OOS) and Inbound Outlyingness Score (IOS). These scores enhance the interpretability of outlier detection results. Both OSs employ graph-, density-, and distribution-based techniques, tailored to high-dimensional data with varying cluster shapes and intensities. OOS evaluates the outlyingness of a point relative to its nearest neighbors, while IOS assesses the total ``influence" a point receives from others within its cluster. Both OSs effectively identify global and local outliers, invariant to data collinearity. Moreover, IOS is robust to the masking problems. With extensive Monte Carlo simulations, we compare the performance of both OSs with CCD-based, traditional, and state-of-the-art outlier detection methods. Both OSs exhibit substantial overall improvements over the CCD-based methods in both artificial and real-world data sets, particularly with IOS, which delivers the best overall performance among all the methods, especially in high-dimensional settings. Keywords: Outlier detection, Outlyingness score, Graph-based clustering, Cluster catch digraphs, High-dimensional data.

Cluster Catch Digraphs with the Nearest Neighbor Distance

We introduce a new method for clustering based on Cluster Catch Digraphs (CCDs). The new method addresses the limitations of RK-CCDs by employing a new variant of spatial randomness test that employs the nearest neighbor distance (NND) instead of the Ripley's K function used by RK-CCDs. We conduct a comprehensive Monte Carlo analysis to assess the performance of our method, considering factors such as dimensionality, data set size, number of clusters, cluster volumes, and inter-cluster distance. Our method is particularly effective for high-dimensional data sets, comparable to or outperforming KS-CCDs and RK-CCDs that rely on a KS-type statistic or the Ripley's K function. We also evaluate our methods using real and complex data sets, comparing them to well-known clustering methods. Again, our methods exhibit competitive performance, producing high-quality clusters with desirable properties. Keywords: Graph-based clustering, Cluster catch digraphs, High-dimensional data, The nearest neighbor distance, Spatial randomness test

Outlier Detection with Cluster Catch Digraphs

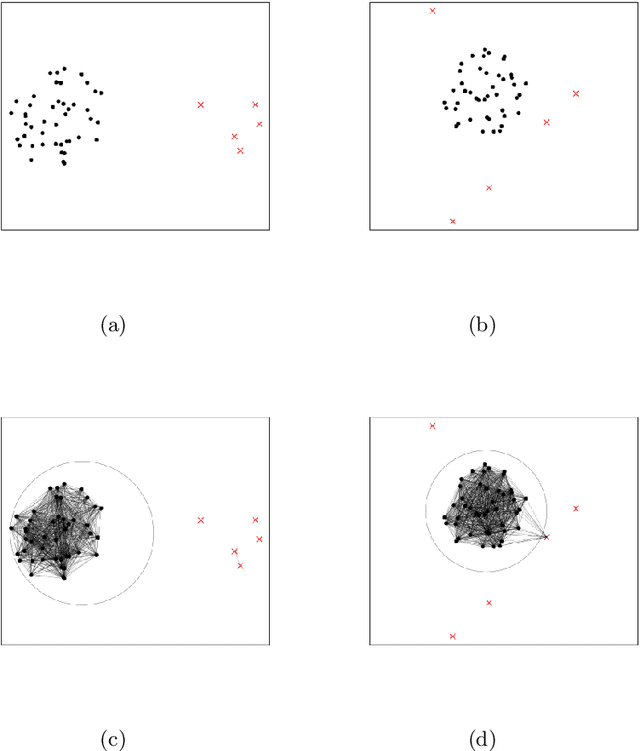
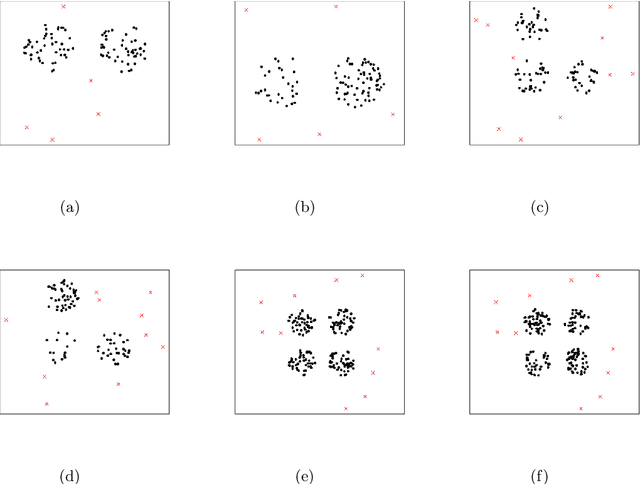
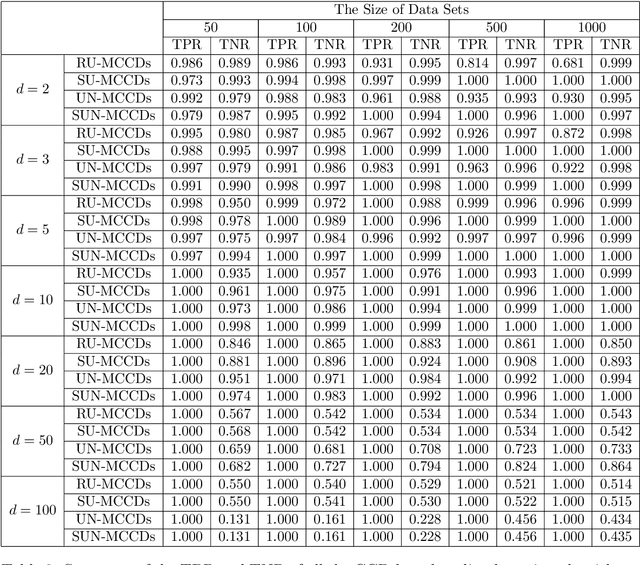
This paper introduces a novel family of outlier detection algorithms based on Cluster Catch Digraphs (CCDs), specifically tailored to address the challenges of high dimensionality and varying cluster shapes, which deteriorate the performance of most traditional outlier detection methods. We propose the Uniformity-Based CCD with Mutual Catch Graph (U-MCCD), the Uniformity- and Neighbor-Based CCD with Mutual Catch Graph (UN-MCCD), and their shape-adaptive variants (SU-MCCD and SUN-MCCD), which are designed to detect outliers in data sets with arbitrary cluster shapes and high dimensions. We present the advantages and shortcomings of these algorithms and provide the motivation or need to define each particular algorithm. Through comprehensive Monte Carlo simulations, we assess their performance and demonstrate the robustness and effectiveness of our algorithms across various settings and contamination levels. We also illustrate the use of our algorithms on various real-life data sets. The U-MCCD algorithm efficiently identifies outliers while maintaining high true negative rates, and the SU-MCCD algorithm shows substantial improvement in handling non-uniform clusters. Additionally, the UN-MCCD and SUN-MCCD algorithms address the limitations of existing methods in high-dimensional spaces by utilizing Nearest Neighbor Distances (NND) for clustering and outlier detection. Our results indicate that these novel algorithms offer substantial advancements in the accuracy and adaptability of outlier detection, providing a valuable tool for various real-world applications. Keyword: Outlier detection, Graph-based clustering, Cluster catch digraphs, $k$-nearest-neighborhood, Mutual catch graphs, Nearest neighbor distance.