Classification Using Proximity Catch Digraphs (Technical Report)
Paper and Code
May 22, 2017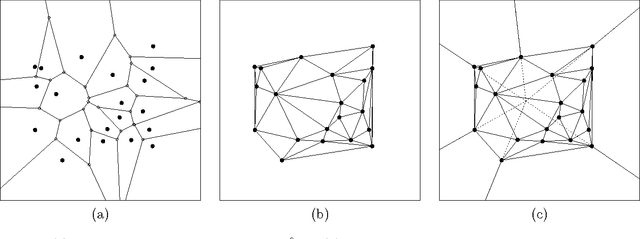
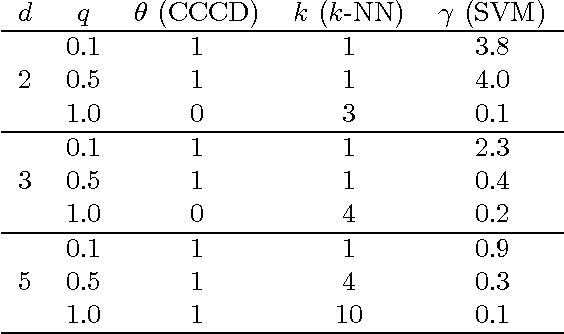
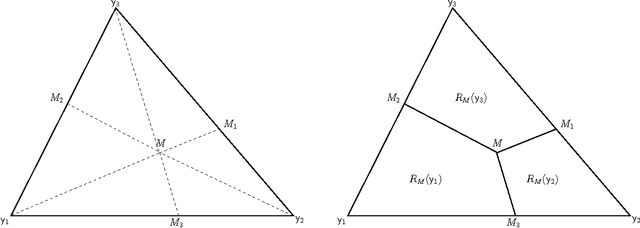
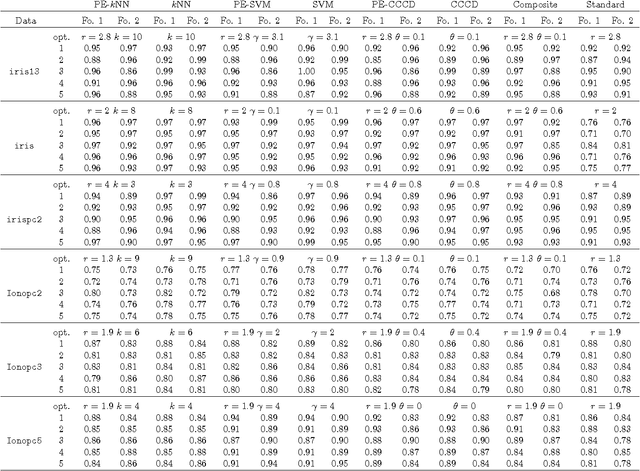
We employ random geometric digraphs to construct semi-parametric classifiers. These data-random digraphs are from parametrized random digraph families called proximity catch digraphs (PCDs). A related geometric digraph family, class cover catch digraph (CCCD), has been used to solve the class cover problem by using its approximate minimum dominating set. CCCDs showed relatively good performance in the classification of imbalanced data sets, and although CCCDs have a convenient construction in $\mathbb{R}^d$, finding minimum dominating sets is NP-hard and its probabilistic behaviour is not mathematically tractable except for $d=1$. On the other hand, a particular family of PCDs, called \emph{proportional-edge} PCDs (PE-PCDs), has mathematical tractable minimum dominating sets in $\mathbb{R}^d$; however their construction in higher dimensions may be computationally demanding. More specifically, we show that the classifiers based on PE-PCDs are prototype-based classifiers such that the exact minimum number of prototypes (equivalent to minimum dominating sets) are found in polynomial time on the number of observations. We construct two types of classifiers based on PE-PCDs. One is a family of hybrid classifiers depend on the location of the points of the training data set, and another type is a family of classifiers solely based on class covers. We assess the classification performance of our PE-PCD based classifiers by extensive Monte Carlo simulations, and compare them with that of other commonly used classifiers. We also show that, similar to CCCD classifiers, our classifiers are relatively better in classification in the presence of class imbalance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge