Long Document Summarization in a Low Resource Setting using Pretrained Language Models

Abstractive summarization is the task of compressing a long document into a coherent short document while retaining salient information. Modern abstractive summarization methods are based on deep neural networks which often require large training datasets. Since collecting summarization datasets is an expensive and time-consuming task, practical industrial settings are usually low-resource. In this paper, we study a challenging low-resource setting of summarizing long legal briefs with an average source document length of 4268 words and only 120 available (document, summary) pairs. To account for data scarcity, we used a modern pretrained abstractive summarizer BART (Lewis et al., 2020), which only achieves 17.9 ROUGE-L as it struggles with long documents. We thus attempt to compress these long documents by identifying salient sentences in the source which best ground the summary, using a novel algorithm based on GPT-2 (Radford et al., 2019) language model perplexity scores, that operates within the low resource regime. On feeding the compressed documents to BART, we observe a 6.0 ROUGE-L improvement. Our method also beats several competitive salience detection baselines. Furthermore, the identified salient sentences tend to agree with an independent human labeling by domain experts.

Incorporating Type II Error Probabilities from Independence Tests into Score-Based Learning of Bayesian Network Structure

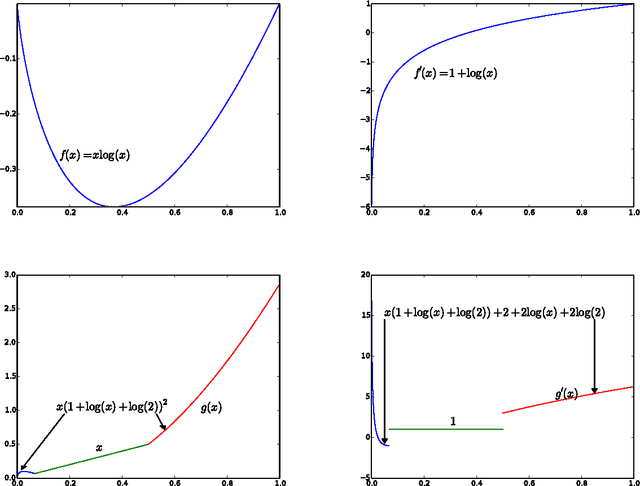
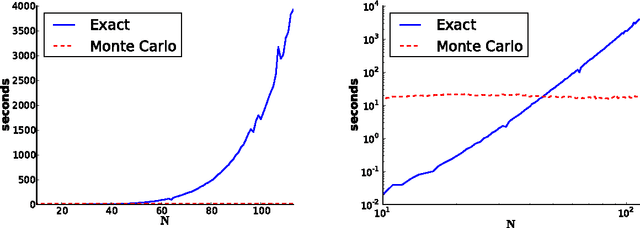
We give a new consistent scoring function for structure learning of Bayesian networks. In contrast to traditional approaches to score-based structure learning, such as BDeu or MDL, the complexity penalty that we propose is data-dependent and is given by the probability that a conditional independence test correctly shows that an edge cannot exist. What really distinguishes this new scoring function from earlier work is that it has the property of becoming computationally easier to maximize as the amount of data increases. We prove a polynomial sample complexity result, showing that maximizing this score is guaranteed to correctly learn a structure with no false edges and a distribution close to the generating distribution, whenever there exists a Bayesian network which is a perfect map for the data generating distribution. Although the new score can be used with any search algorithm, in our related UAI 2013 paper [BS13], we have given empirical results showing that it is particularly effective when used together with a linear programming relaxation approach to Bayesian network structure learning. The present paper contains all details of the proofs of the finite-sample complexity results in [BS13] as well as detailed explanation of the computation of the certain error probabilities called beta-values, whose precomputation and tabulation is necessary for the implementation of the algorithm in [BS13].

SparsityBoost: A New Scoring Function for Learning Bayesian Network Structure

We give a new consistent scoring function for structure learning of Bayesian networks. In contrast to traditional approaches to scorebased structure learning, such as BDeu or MDL, the complexity penalty that we propose is data-dependent and is given by the probability that a conditional independence test correctly shows that an edge cannot exist. What really distinguishes this new scoring function from earlier work is that it has the property of becoming computationally easier to maximize as the amount of data increases. We prove a polynomial sample complexity result, showing that maximizing this score is guaranteed to correctly learn a structure with no false edges and a distribution close to the generating distribution, whenever there exists a Bayesian network which is a perfect map for the data generating distribution. Although the new score can be used with any search algorithm, we give empirical results showing that it is particularly effective when used together with a linear programming relaxation approach to Bayesian network structure learning.