Incorporating Type II Error Probabilities from Independence Tests into Score-Based Learning of Bayesian Network Structure

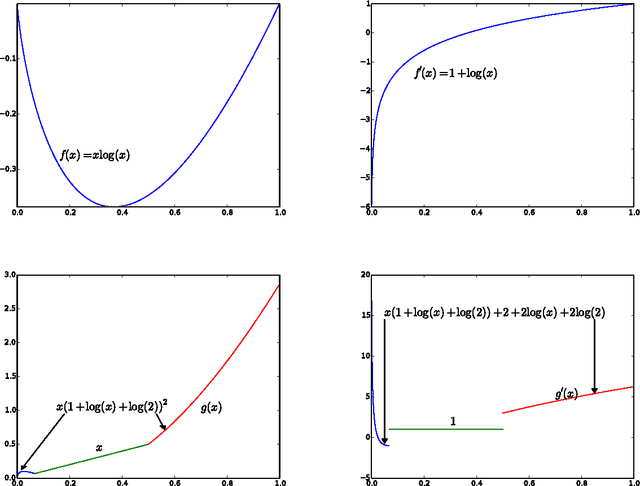
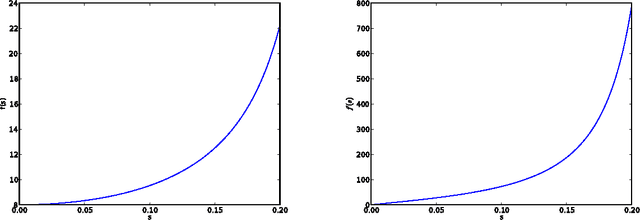
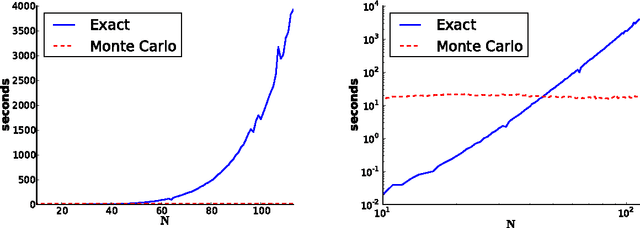
We give a new consistent scoring function for structure learning of Bayesian networks. In contrast to traditional approaches to score-based structure learning, such as BDeu or MDL, the complexity penalty that we propose is data-dependent and is given by the probability that a conditional independence test correctly shows that an edge cannot exist. What really distinguishes this new scoring function from earlier work is that it has the property of becoming computationally easier to maximize as the amount of data increases. We prove a polynomial sample complexity result, showing that maximizing this score is guaranteed to correctly learn a structure with no false edges and a distribution close to the generating distribution, whenever there exists a Bayesian network which is a perfect map for the data generating distribution. Although the new score can be used with any search algorithm, in our related UAI 2013 paper [BS13], we have given empirical results showing that it is particularly effective when used together with a linear programming relaxation approach to Bayesian network structure learning. The present paper contains all details of the proofs of the finite-sample complexity results in [BS13] as well as detailed explanation of the computation of the certain error probabilities called beta-values, whose precomputation and tabulation is necessary for the implementation of the algorithm in [BS13].