Training Artificial Neural Networks by Coordinate Search Algorithm

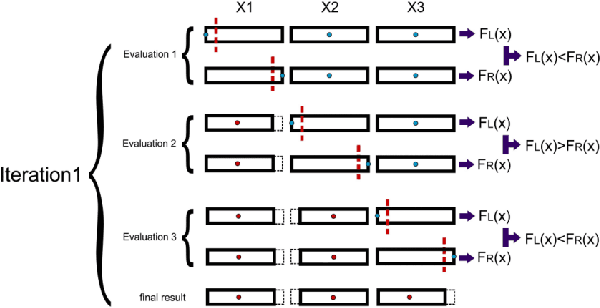
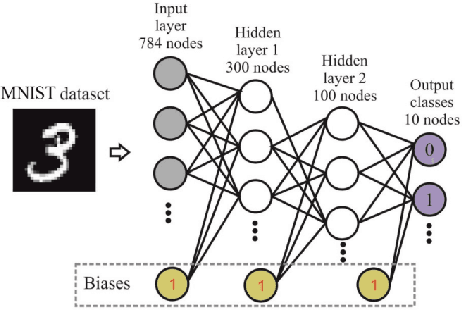
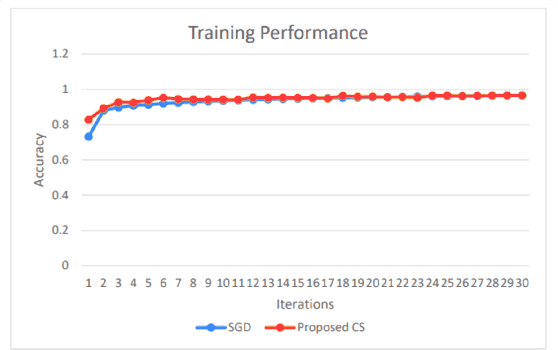
Training Artificial Neural Networks poses a challenging and critical problem in machine learning. Despite the effectiveness of gradient-based learning methods, such as Stochastic Gradient Descent (SGD), in training neural networks, they do have several limitations. For instance, they require differentiable activation functions, and cannot optimize a model based on several independent non-differentiable loss functions simultaneously; for example, the F1-score, which is used during testing, can be used during training when a gradient-free optimization algorithm is utilized. Furthermore, the training in any DNN can be possible with a small size of the training dataset. To address these concerns, we propose an efficient version of the gradient-free Coordinate Search (CS) algorithm, an instance of General Pattern Search methods, for training neural networks. The proposed algorithm can be used with non-differentiable activation functions and tailored to multi-objective/multi-loss problems. Finding the optimal values for weights of ANNs is a large-scale optimization problem. Therefore instead of finding the optimal value for each variable, which is the common technique in classical CS, we accelerate optimization and convergence by bundling the weights. In fact, this strategy is a form of dimension reduction for optimization problems. Based on the experimental results, the proposed method, in some cases, outperforms the gradient-based approach, particularly, in situations with insufficient labeled training data. The performance plots demonstrate a high convergence rate, highlighting the capability of our suggested method to find a reasonable solution with fewer function calls. As of now, the only practical and efficient way of training ANNs with hundreds of thousands of weights is gradient-based algorithms such as SGD or Adam. In this paper we introduce an alternative method for training ANN.