Edwin Pin
Computational Complexity of Preferred Subset Repairs on Data-Graphs
Feb 14, 2024Abstract:The problem of repairing inconsistent knowledge bases has a long history within the communities of database theory and knowledge representation and reasoning, especially from the perspective of structured data. However, as the data available in real-world domains becomes more complex and interconnected, the need naturally arises for developing new types of repositories, representation languages, and semantics, to allow for more suitable ways to query and reason about it. Graph databases provide an effective way to represent relationships among semi-structured data, and allow processing and querying these connections efficiently. In this work, we focus on the problem of computing prioritized repairs over graph databases with data values, using a notion of consistency based on Reg-GXPath expressions as integrity constraints. We present several preference criteria based on the standard subset repair semantics, incorporating weights, multisets, and set-based priority levels. We study the most common repairing tasks, showing that it is possible to maintain the same computational complexity as in the case where no preference criterion is available for exploitation. To complete the picture, we explore the complexity of consistent query answering in this setting and obtain tight lower and upper bounds for all the preference criteria introduced.
PDL on Steroids: on Expressive Extensions of PDL with Intersection and Converse
Apr 20, 2023Abstract:We introduce CPDL+, a family of expressive logics rooted in Propositional Dynamic Logic (PDL). In terms of expressive power, CPDL+ strictly contains PDL extended with intersection and converse (a.k.a. ICPDL) as well as Conjunctive Queries (CQ), Conjunctive Regular Path Queries (CRPQ), or some known extensions thereof (Regular Queries and CQPDL). We investigate the expressive power, characterization of bisimulation, satisfiability, and model checking for CPDL+. We argue that natural subclasses of CPDL+ can be defined in terms of the tree-width of the underlying graphs of the formulas. We show that the class of CPDL+ formulas of tree-width 2 is equivalent to ICPDL, and that it also coincides with CPDL+ formulas of tree-width 1. However, beyond tree-width 2, incrementing the tree-width strictly increases the expressive power. We characterize the expressive power for every class of fixed tree-width formulas in terms of a bisimulation game with pebbles. Based on this characterization, we show that CPDL+ has a tree-like model property. We prove that the satisfiability problem is decidable in 2ExpTime on fixed tree-width formulas, coinciding with the complexity of ICPDL. We also exhibit classes for which satisfiability is reduced to ExpTime. Finally, we establish that the model checking problem for fixed tree-width formulas is in \ptime, contrary to the full class CPDL+.
On the complexity of finding set repairs for data-graphs
Jun 15, 2022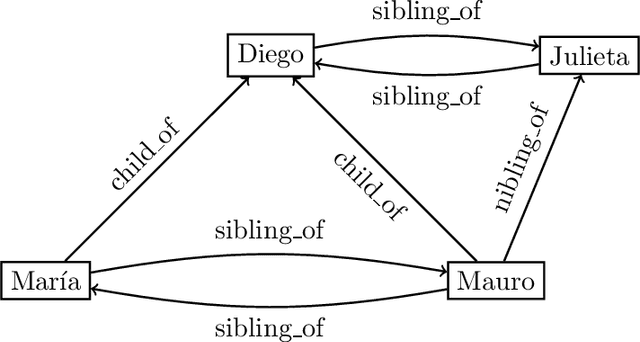
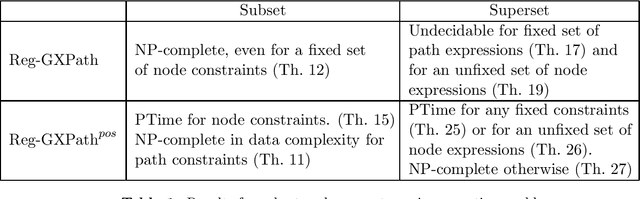
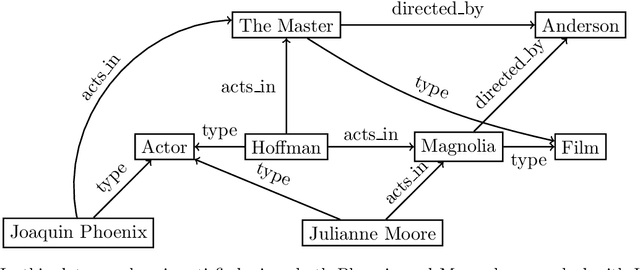
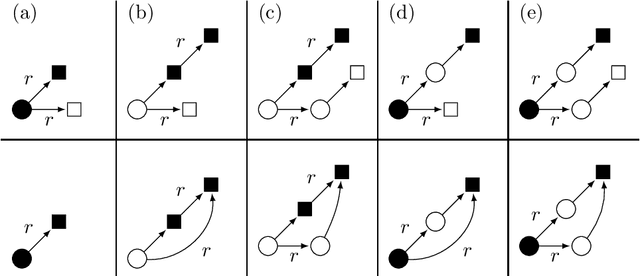
Abstract:In the deeply interconnected world we live in, pieces of information link domains all around us. As graph databases embrace effectively relationships among data and allow processing and querying these connections efficiently, they are rapidly becoming a popular platform for storage that supports a wide range of domains and applications. As in the relational case, it is expected that data preserves a set of integrity constraints that define the semantic structure of the world it represents. When a database does not satisfy its integrity constraints, a possible approach is to search for a 'similar' database that does satisfy the constraints, also known as a repair. In this work, we study the problem of computing subset and superset repairs for graph databases with data values using a notion of consistency based on a set of Reg-GXPath expressions as integrity constraints. We show that for positive fragments of Reg-GXPath these problems admit a polynomial-time algorithm, while the full expressive power of the language renders them intractable.
An epistemic approach to model uncertainty in data-graphs
Sep 29, 2021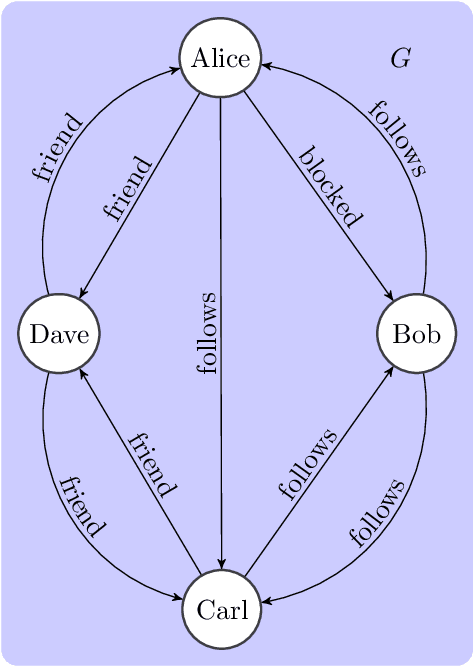
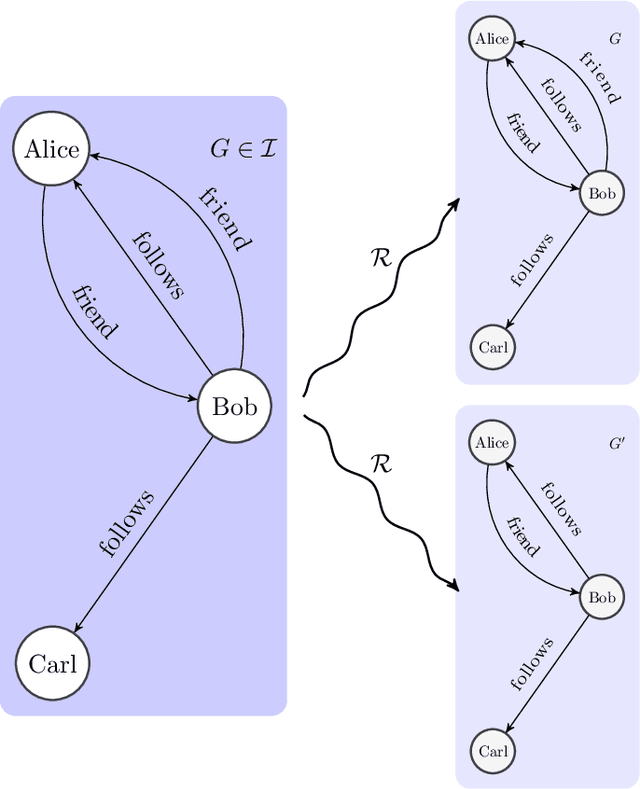
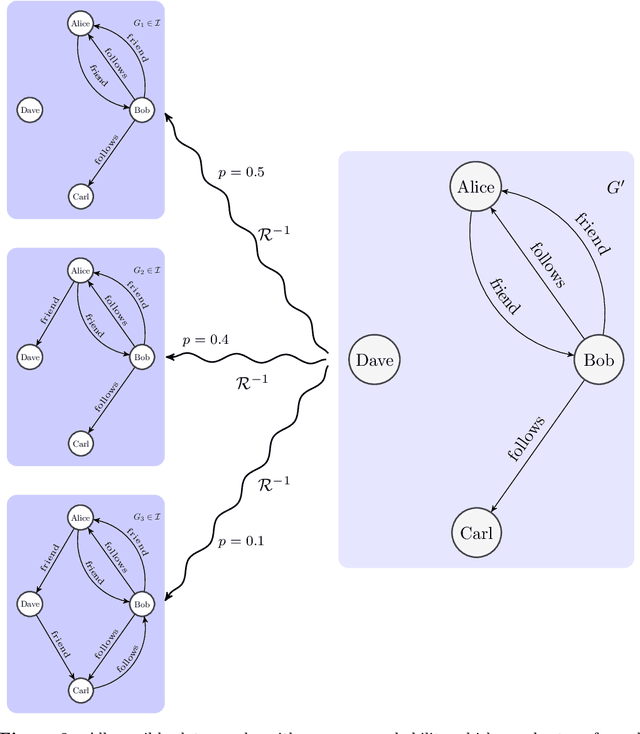
Abstract:Graph databases are becoming widely successful as data models that allow to effectively represent and process complex relationships among various types of data. As with any other type of data repository, graph databases may suffer from errors and discrepancies with respect to the real-world data they intend to represent. In this work we explore the notion of probabilistic unclean graph databases, previously proposed for relational databases, in order to capture the idea that the observed (unclean) graph database is actually the noisy version of a clean one that correctly models the world but that we know partially. As the factors that may be involved in the observation can be many, e.g, all different types of clerical errors or unintended transformations of the data, we assume a probabilistic model that describes the distribution over all possible ways in which the clean (uncertain) database could have been polluted. Based on this model we define two computational problems: data cleaning and probabilistic query answering and study for both of them their corresponding complexity when considering that the transformation of the database can be caused by either removing (subset) or adding (superset) nodes and edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge