PDL on Steroids: on Expressive Extensions of PDL with Intersection and Converse

We introduce CPDL+, a family of expressive logics rooted in Propositional Dynamic Logic (PDL). In terms of expressive power, CPDL+ strictly contains PDL extended with intersection and converse (a.k.a. ICPDL) as well as Conjunctive Queries (CQ), Conjunctive Regular Path Queries (CRPQ), or some known extensions thereof (Regular Queries and CQPDL). We investigate the expressive power, characterization of bisimulation, satisfiability, and model checking for CPDL+. We argue that natural subclasses of CPDL+ can be defined in terms of the tree-width of the underlying graphs of the formulas. We show that the class of CPDL+ formulas of tree-width 2 is equivalent to ICPDL, and that it also coincides with CPDL+ formulas of tree-width 1. However, beyond tree-width 2, incrementing the tree-width strictly increases the expressive power. We characterize the expressive power for every class of fixed tree-width formulas in terms of a bisimulation game with pebbles. Based on this characterization, we show that CPDL+ has a tree-like model property. We prove that the satisfiability problem is decidable in 2ExpTime on fixed tree-width formulas, coinciding with the complexity of ICPDL. We also exhibit classes for which satisfiability is reduced to ExpTime. Finally, we establish that the model checking problem for fixed tree-width formulas is in \ptime, contrary to the full class CPDL+.

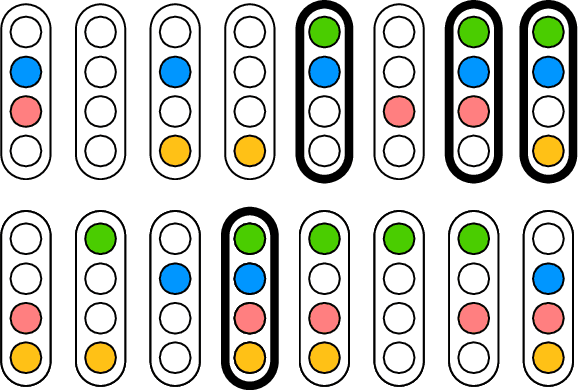
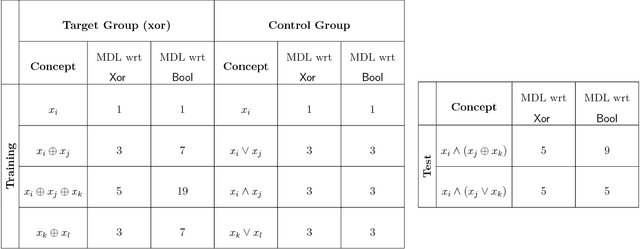
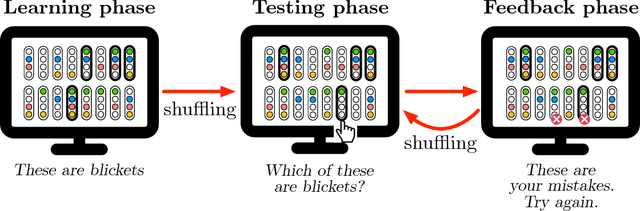
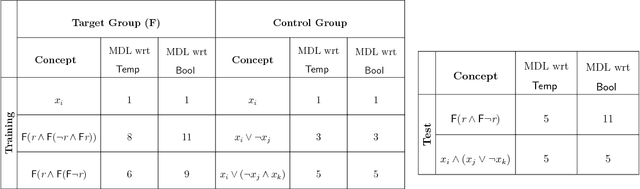
Learning is Compiling: Experience Shapes Concept Learning by Combining Primitives in a Language of Thought

Recent approaches to human concept learning have successfully combined the power of symbolic, infinitely productive, rule systems and statistical learning. The aim of most of these studies is to reveal the underlying language structuring these representations and providing a general substrate for thought. Here, we ask about the plasticity of symbolic descriptive languages. We perform two concept learning experiments, that consistently demonstrate that humans can change very rapidly the repertoire of symbols they use to identify concepts, by compiling expressions which are frequently used into new symbols of the language. The pattern of concept learning times is accurately described by a Bayesian agent that rationally updates the probability of compiling a new expression according to how useful it has been to compress concepts so far. By portraying the Language of Thought as a flexible system of rules, we also highlight the intrinsic difficulties to pin it down empirically.

LT^2C^2: A language of thought with Turing-computable Kolmogorov complexity

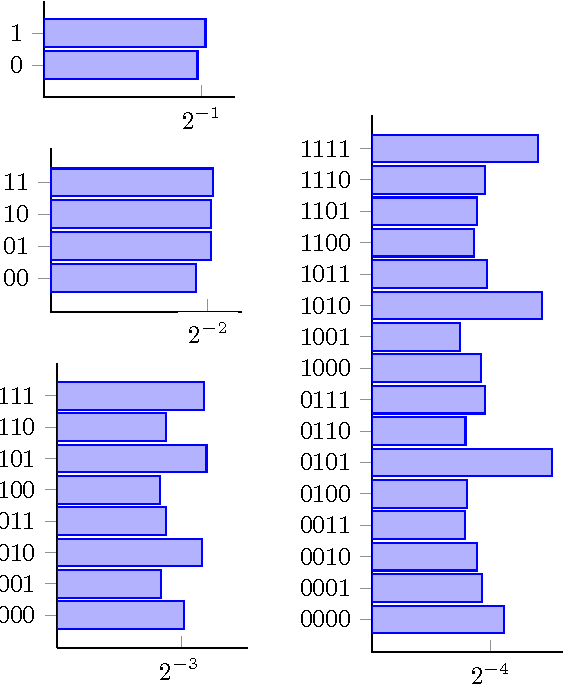
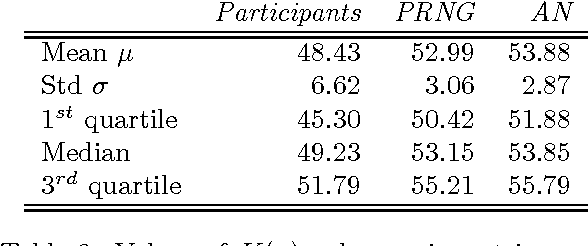
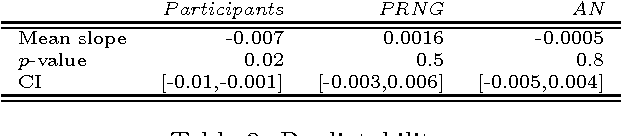
In this paper, we present a theoretical effort to connect the theory of program size to psychology by implementing a concrete language of thought with Turing-computable Kolmogorov complexity (LT^2C^2) satisfying the following requirements: 1) to be simple enough so that the complexity of any given finite binary sequence can be computed, 2) to be based on tangible operations of human reasoning (printing, repeating,...), 3) to be sufficiently powerful to generate all possible sequences but not too powerful as to identify regularities which would be invisible to humans. We first formalize LT^2C^2, giving its syntax and semantics and defining an adequate notion of program size. Our setting leads to a Kolmogorov complexity function relative to LT^2C^2 which is computable in polynomial time, and it also induces a prediction algorithm in the spirit of Solomonoff's inductive inference theory. We then prove the efficacy of this language by investigating regularities in strings produced by participants attempting to generate random strings. Participants had a profound understanding of randomness and hence avoided typical misconceptions such as exaggerating the number of alternations. We reasoned that remaining regularities would express the algorithmic nature of human thoughts, revealed in the form of specific patterns. Kolmogorov complexity relative to LT^2C^2 passed three expected tests examined here: 1) human sequences were less complex than control PRNG sequences, 2) human sequences were not stationary, showing decreasing values of complexity resulting from fatigue, 3) each individual showed traces of algorithmic stability since fitting of partial sequences was more effective to predict subsequent sequences than average fits. This work extends on previous efforts to combine notions of Kolmogorov complexity theory and algorithmic information theory to psychology, by explicitly ...