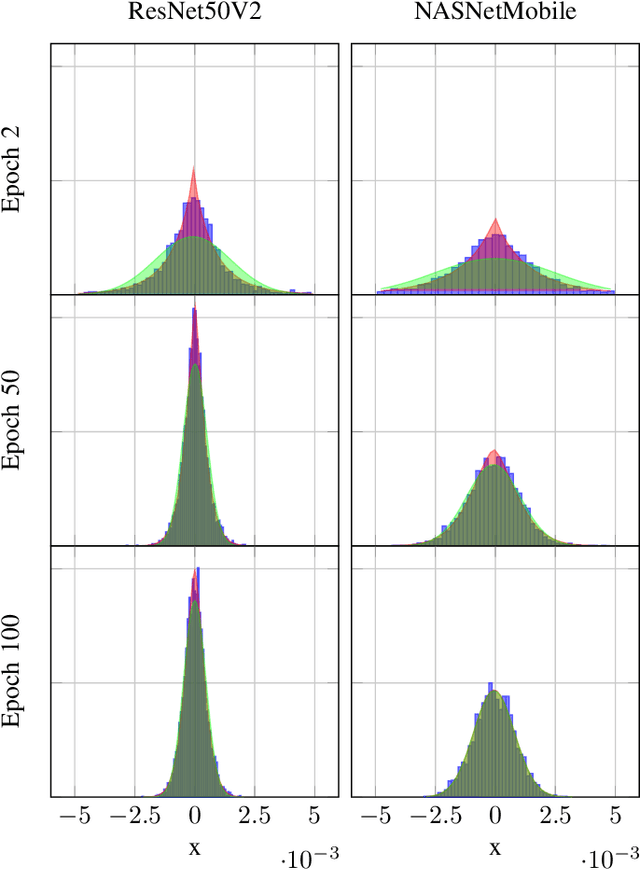
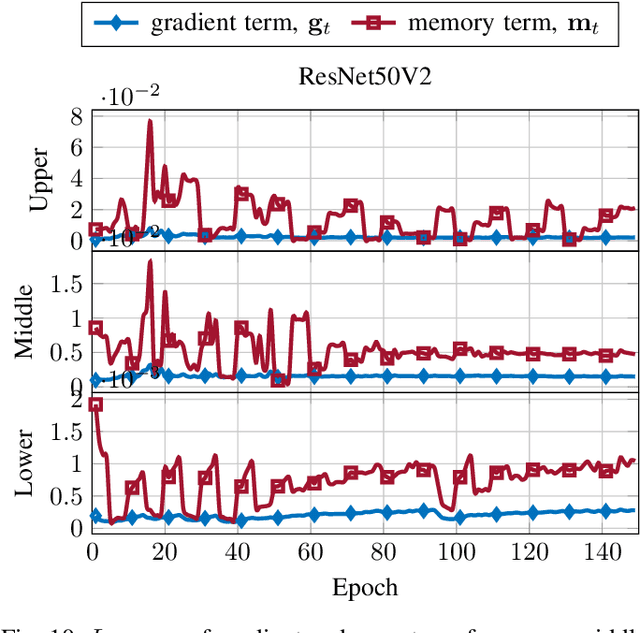
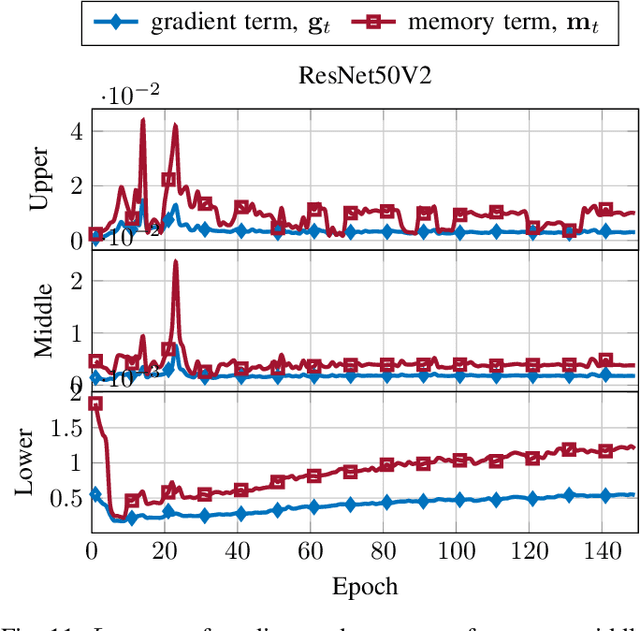
How to Attain Communication-Efficient DNN Training? Convert, Compress, Correct

In this paper, we introduce $\mathsf{CO}_3$, an algorithm for communication-efficiency federated Deep Neural Network (DNN) training.$\mathsf{CO}_3$ takes its name from three processing applied steps which reduce the communication load when transmitting the local gradients from the remote users to the Parameter Server.Namely:(i) gradient quantization through floating-point conversion, (ii) lossless compression of the quantized gradient, and (iii) quantization error correction.We carefully design each of the steps above so as to minimize the loss in the distributed DNN training when the communication overhead is fixed.In particular, in the design of steps (i) and (ii), we adopt the assumption that DNN gradients are distributed according to a generalized normal distribution.This assumption is validated numerically in the paper. For step (iii), we utilize an error feedback with memory decay mechanism to correct the quantization error introduced in step (i). We argue that this coefficient, similarly to the learning rate, can be optimally tuned to improve convergence. The performance of $\mathsf{CO}_3$ is validated through numerical simulations and is shown having better accuracy and improved stability at a reduced communication payload.

Convert, compress, correct: Three steps toward communication-efficient DNN training

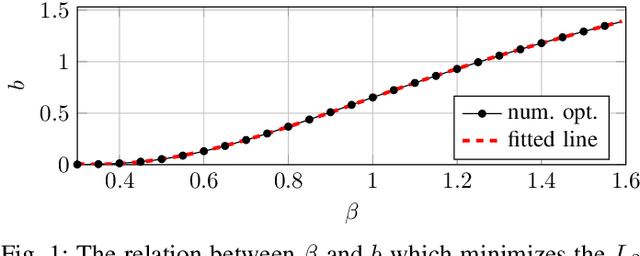
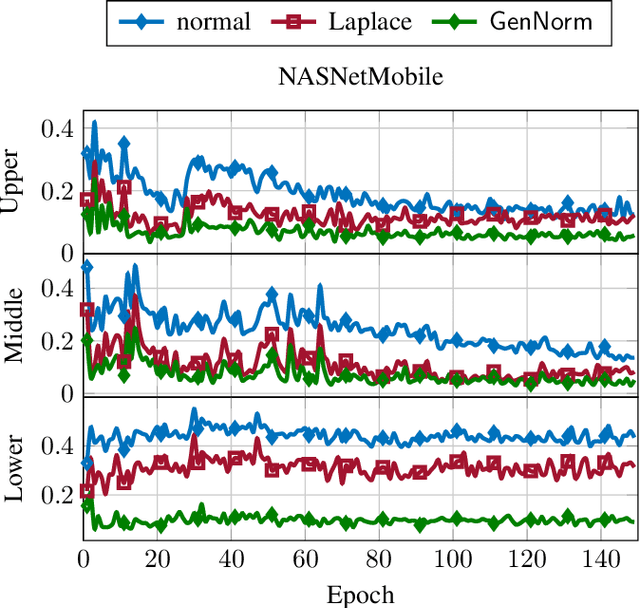
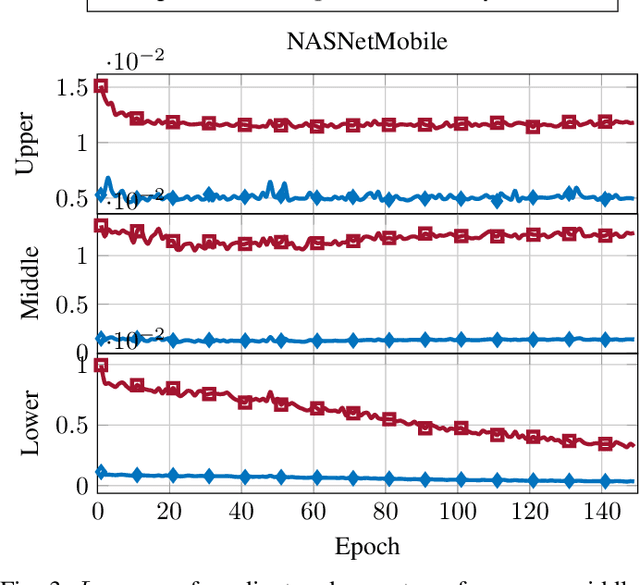
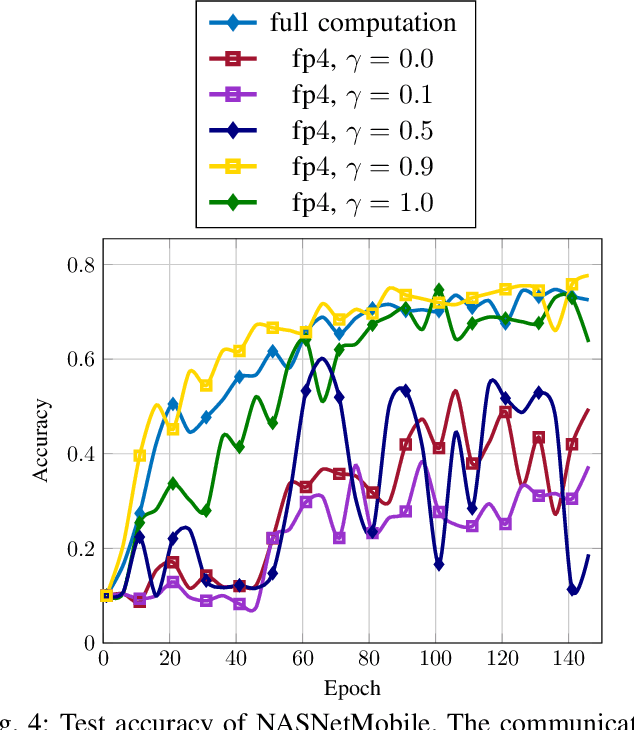
In this paper, we introduce a novel algorithm, $\mathsf{CO}_3$, for communication-efficiency distributed Deep Neural Network (DNN) training. $\mathsf{CO}_3$ is a joint training/communication protocol, which encompasses three processing steps for the network gradients: (i) quantization through floating-point conversion, (ii) lossless compression, and (iii) error correction. These three components are crucial in the implementation of distributed DNN training over rate-constrained links. The interplay of these three steps in processing the DNN gradients is carefully balanced to yield a robust and high-performance scheme. The performance of the proposed scheme is investigated through numerical evaluations over CIFAR-10.

DNN gradient lossless compression: Can GenNorm be the answer?

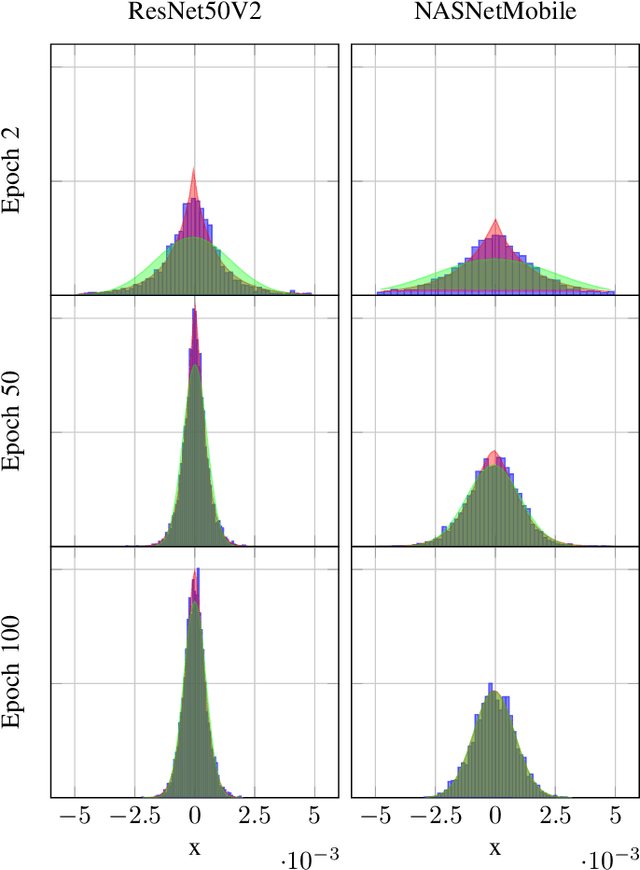
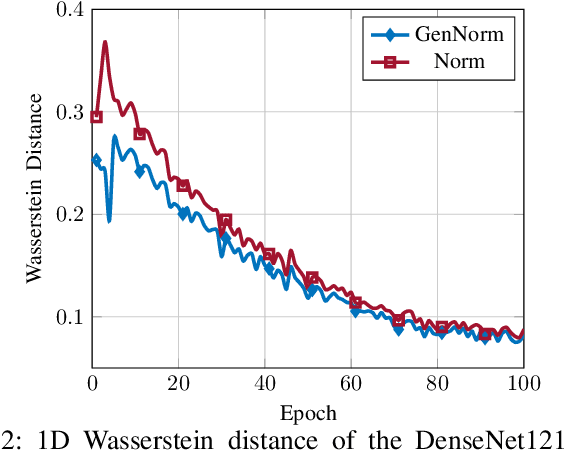
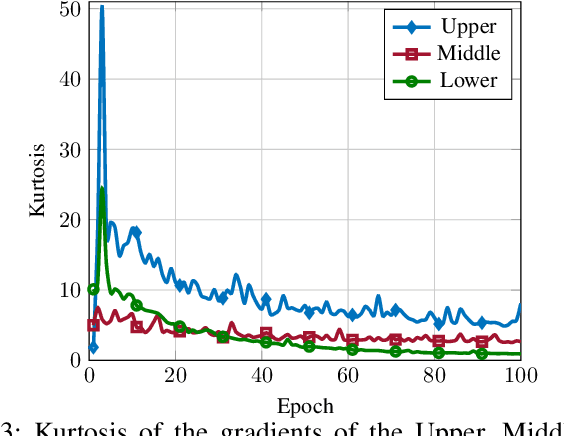
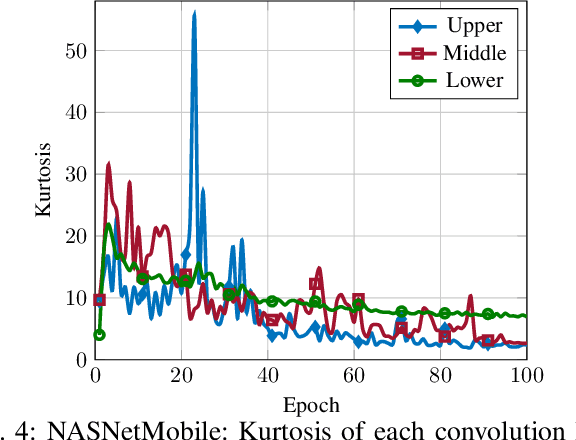
In this paper, the problem of optimal gradient lossless compression in Deep Neural Network (DNN) training is considered. Gradient compression is relevant in many distributed DNN training scenarios, including the recently popular federated learning (FL) scenario in which each remote users are connected to the parameter server (PS) through a noiseless but rate limited channel. In distributed DNN training, if the underlying gradient distribution is available, classical lossless compression approaches can be used to reduce the number of bits required for communicating the gradient entries. Mean field analysis has suggested that gradient updates can be considered as independent random variables, while Laplace approximation can be used to argue that gradient has a distribution approximating the normal (Norm) distribution in some regimes. In this paper we argue that, for some networks of practical interest, the gradient entries can be well modelled as having a generalized normal (GenNorm) distribution. We provide numerical evaluations to validate that the hypothesis GenNorm modelling provides a more accurate prediction of the DNN gradient tail distribution. Additionally, this modeling choice provides concrete improvement in terms of lossless compression of the gradients when applying classical fix-to-variable lossless coding algorithms, such as Huffman coding, to the quantized gradient updates. This latter results indeed provides an effective compression strategy with low memory and computational complexity that has great practical relevance in distributed DNN training scenarios.

Speeding-Up Back-Propagation in DNN: Approximate Outer Product with Memory

In this paper, an algorithm for approximate evaluation of back-propagation in DNN training is considered, which we term Approximate Outer Product Gradient Descent with Memory (Mem-AOP-GD). The Mem-AOP-GD algorithm implements an approximation of the stochastic gradient descent by considering only a subset of the outer products involved in the matrix multiplications that encompass backpropagation. In order to correct for the inherent bias in this approximation, the algorithm retains in memory an accumulation of the outer products that are not used in the approximation. We investigate the performance of the proposed algorithm in terms of DNN training loss under two design parameters: (i) the number of outer products used for the approximation, and (ii) the policy used to select such outer products. We experimentally show that significant improvements in computational complexity as well as accuracy can indeed be obtained through Mem-AOPGD.