Information-Theoretic Optimization for Task-Adapted Compressed Sensing Magnetic Resonance Imaging

Task-adapted compressed sensing magnetic resonance imaging (CS-MRI) is emerging to address the specific demands of downstream clinical tasks with significantly fewer k-space measurements than required by Nyquist sampling. However, existing task-adapted CS-MRI methods suffer from the uncertainty problem for medical diagnosis and cannot achieve adaptive sampling in end-to-end optimization with reconstruction or clinical tasks. To address these limitations, we propose the first task-adapted CS-MRI from the information-theoretic perspective to simultaneously achieve probabilistic inference for uncertainty prediction and adapt to arbitrary sampling ratios and versatile clinical applications. Specifically, we formalize the task-adapted CS-MRI optimization problem by maximizing the mutual information between undersampled k-space measurements and clinical tasks to enable probabilistic inference for addressing the uncertainty problem. We leverage amortized optimization and construct tractable variational bounds for mutual information to jointly optimize sampling, reconstruction, and task-inference models, which enables flexible sampling ratio control using a single end-to-end trained model. Furthermore, the proposed framework addresses two kinds of distinct clinical scenarios within a unified approach, i.e., i) joint task and reconstruction, where reconstruction serves as an auxiliary process to enhance task performance; and ii) task implementation with suppressed reconstruction, applicable for privacy protection. Extensive experiments on large-scale MRI datasets demonstrate that the proposed framework achieves highly competitive performance on standard metrics like Dice compared to deterministic counterpart but provides better distribution matching to the ground-truth posterior distribution as measured by the generalized energy distance (GED).

Point Cloud Resampling with Learnable Heat Diffusion

Generative diffusion models have shown empirical successes in point cloud resampling, generating a denser and more uniform distribution of points from sparse or noisy 3D point clouds by progressively refining noise into structure. However, existing diffusion models employ manually predefined schemes, which often fail to recover the underlying point cloud structure due to the rigid and disruptive nature of the geometric degradation. To address this issue, we propose a novel learnable heat diffusion framework for point cloud resampling, which directly parameterizes the marginal distribution for the forward process by learning the adaptive heat diffusion schedules and local filtering scales of the time-varying heat kernel, and consequently, generates an adaptive conditional prior for the reverse process. Unlike previous diffusion models with a fixed prior, the adaptive conditional prior selectively preserves geometric features of the point cloud by minimizing a refined variational lower bound, guiding the points to evolve towards the underlying surface during the reverse process. Extensive experimental results demonstrate that the proposed point cloud resampling achieves state-of-the-art performance in representative reconstruction tasks including point cloud denoising and upsampling.

Point Cloud Denoising With Fine-Granularity Dynamic Graph Convolutional Networks

Due to limitations in acquisition equipment, noise perturbations often corrupt 3-D point clouds, hindering down-stream tasks such as surface reconstruction, rendering, and further processing. Existing 3-D point cloud denoising methods typically fail to reliably fit the underlying continuous surface, resulting in a degradation of reconstruction performance. This paper introduces fine-granularity dynamic graph convolutional networks called GD-GCN, a novel approach to denoising in 3-D point clouds. The GD-GCN employs micro-step temporal graph convolution (MST-GConv) to perform feature learning in a gradual manner. Compared with the conventional GCN, which commonly uses discrete integer-step graph convolution, this modification introduces a more adaptable and nuanced approach to feature learning within graph convolution networks. It more accurately depicts the process of fitting the point cloud with noise to the underlying surface by and the learning process for MST-GConv acts like a changing system and is managed through a type of neural network known as neural Partial Differential Equations (PDEs). This means it can adapt and improve over time. GD-GCN approximates the Riemannian metric, calculating distances between points along a low-dimensional manifold. This capability allows it to understand the local geometric structure and effectively capture diverse relationships between points from different geometric regions through geometric graph construction based on Riemannian distances. Additionally, GD-GCN incorporates robust graph spectral filters based on the Bernstein polynomial approximation, which modulate eigenvalues for complex and arbitrary spectral responses, providing theoretical guarantees for BIBO stability. Symmetric channel mixing matrices further enhance filter flexibility by enabling channel-level scaling and shifting in the spectral domain.

Hybrid ISTA: Unfolding ISTA With Convergence Guarantees Using Free-Form Deep Neural Networks

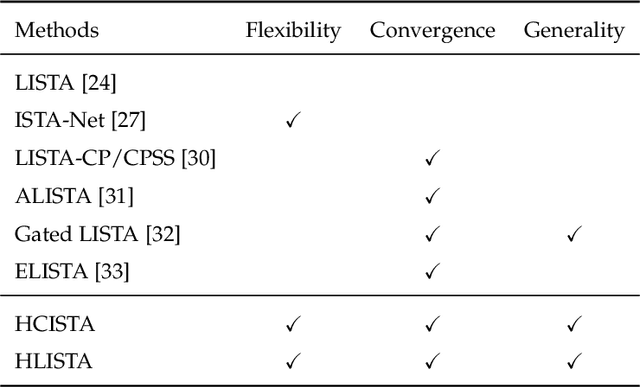
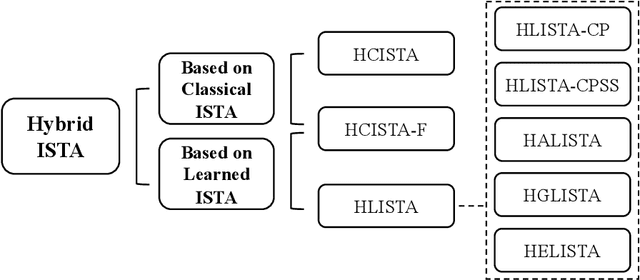
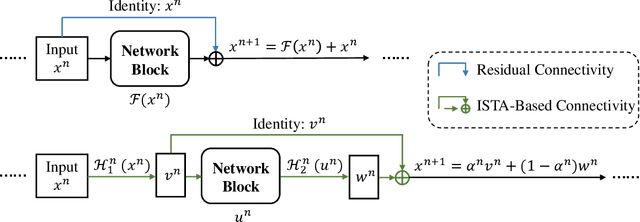
It is promising to solve linear inverse problems by unfolding iterative algorithms (e.g., iterative shrinkage thresholding algorithm (ISTA)) as deep neural networks (DNNs) with learnable parameters. However, existing ISTA-based unfolded algorithms restrict the network architectures for iterative updates with the partial weight coupling structure to guarantee convergence. In this paper, we propose hybrid ISTA to unfold ISTA with both pre-computed and learned parameters by incorporating free-form DNNs (i.e., DNNs with arbitrary feasible and reasonable network architectures), while ensuring theoretical convergence. We first develop HCISTA to improve the efficiency and flexibility of classical ISTA (with pre-computed parameters) without compromising the convergence rate in theory. Furthermore, the DNN-based hybrid algorithm is generalized to popular variants of learned ISTA, dubbed HLISTA, to enable a free architecture of learned parameters with a guarantee of linear convergence. To our best knowledge, this paper is the first to provide a convergence-provable framework that enables free-form DNNs in ISTA-based unfolded algorithms. This framework is general to endow arbitrary DNNs for solving linear inverse problems with convergence guarantees. Extensive experiments demonstrate that hybrid ISTA can reduce the reconstruction error with an improved convergence rate in the tasks of sparse recovery and compressive sensing.