Hybrid ISTA: Unfolding ISTA With Convergence Guarantees Using Free-Form Deep Neural Networks
Paper and Code
May 05, 2022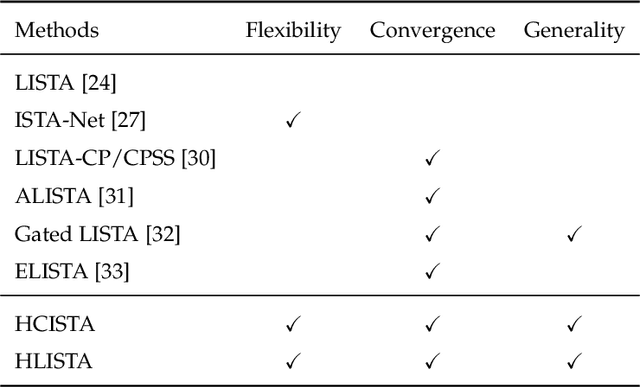
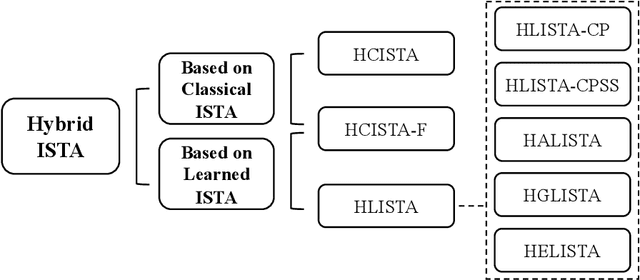
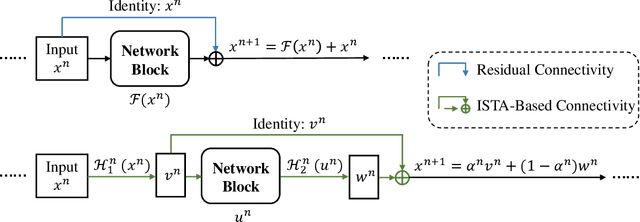

It is promising to solve linear inverse problems by unfolding iterative algorithms (e.g., iterative shrinkage thresholding algorithm (ISTA)) as deep neural networks (DNNs) with learnable parameters. However, existing ISTA-based unfolded algorithms restrict the network architectures for iterative updates with the partial weight coupling structure to guarantee convergence. In this paper, we propose hybrid ISTA to unfold ISTA with both pre-computed and learned parameters by incorporating free-form DNNs (i.e., DNNs with arbitrary feasible and reasonable network architectures), while ensuring theoretical convergence. We first develop HCISTA to improve the efficiency and flexibility of classical ISTA (with pre-computed parameters) without compromising the convergence rate in theory. Furthermore, the DNN-based hybrid algorithm is generalized to popular variants of learned ISTA, dubbed HLISTA, to enable a free architecture of learned parameters with a guarantee of linear convergence. To our best knowledge, this paper is the first to provide a convergence-provable framework that enables free-form DNNs in ISTA-based unfolded algorithms. This framework is general to endow arbitrary DNNs for solving linear inverse problems with convergence guarantees. Extensive experiments demonstrate that hybrid ISTA can reduce the reconstruction error with an improved convergence rate in the tasks of sparse recovery and compressive sensing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge