Effect Size Estimation for Duration Recommendation in Online Experiments: Leveraging Hierarchical Models and Objective Utility Approaches

The selection of the assumed effect size (AES) critically determines the duration of an experiment, and hence its accuracy and efficiency. Traditionally, experimenters determine AES based on domain knowledge. However, this method becomes impractical for online experimentation services managing numerous experiments, and a more automated approach is hence of great demand. We initiate the study of data-driven AES selection in for online experimentation services by introducing two solutions. The first employs a three-layer Gaussian Mixture Model considering the heteroskedasticity across experiments, and it seeks to estimate the true expected effect size among positive experiments. The second method, grounded in utility theory, aims to determine the optimal effect size by striking a balance between the experiment's cost and the precision of decision-making. Through comparisons with baseline methods using both simulated and real data, we showcase the superior performance of the proposed approaches.

Experimentation Platforms Meet Reinforcement Learning: Bayesian Sequential Decision-Making for Continuous Monitoring

With the growing needs of online A/B testing to support the innovation in industry, the opportunity cost of running an experiment becomes non-negligible. Therefore, there is an increasing demand for an efficient continuous monitoring service that allows early stopping when appropriate. Classic statistical methods focus on hypothesis testing and are mostly developed for traditional high-stake problems such as clinical trials, while experiments at online service companies typically have very different features and focuses. Motivated by the real needs, in this paper, we introduce a novel framework that we developed in Amazon to maximize customer experience and control opportunity cost. We formulate the problem as a Bayesian optimal sequential decision making problem that has a unified utility function. We discuss extensively practical design choices and considerations. We further introduce how to solve the optimal decision rule via Reinforcement Learning and scale the solution. We show the effectiveness of this novel approach compared with existing methods via a large-scale meta-analysis on experiments in Amazon.

Bayesian Sample Size Prediction for Online Activity

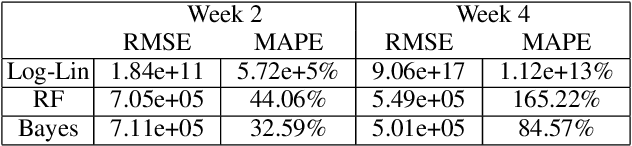
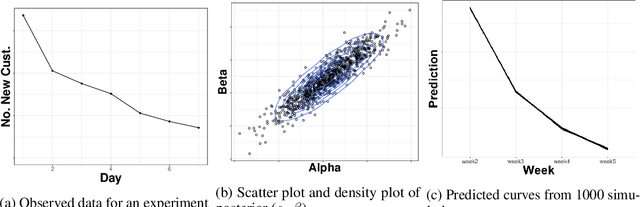
In many contexts it is useful to predict the number of individuals in some population who will initiate a particular activity during a given period. For example, the number of users who will install a software update, the number of customers who will use a new feature on a website or who will participate in an A/B test. In practical settings, there is heterogeneity amongst individuals with regard to the distribution of time until they will initiate. For these reasons it is inappropriate to assume that the number of new individuals observed on successive days will be identically distributed. Given observations on the number of unique users participating in an initial period, we present a simple but novel Bayesian method for predicting the number of additional individuals who will subsequently participate during a subsequent period. We illustrate the performance of the method in predicting sample size in online experimentation.