Do cities have a unique magnetic pulse?

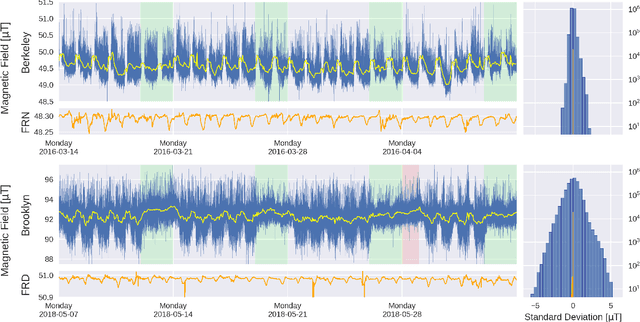
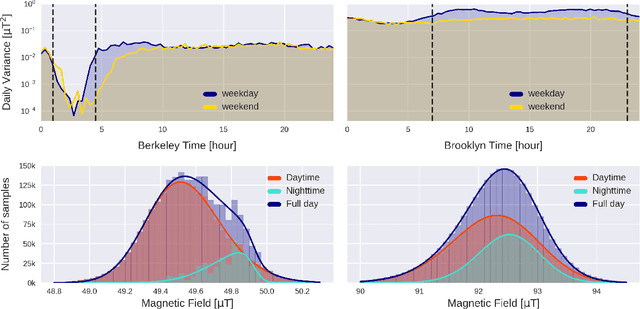
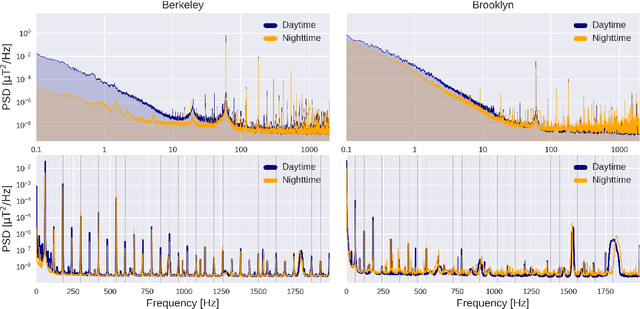
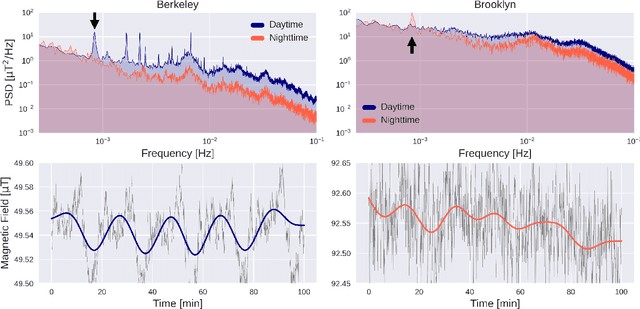
We present a comparative analysis of urban magnetic fields between two American cities: Berkeley (California) and Brooklyn Borough of New York City (New York). Our analysis uses data taken over a four-week period during which magnetic field data were continuously recorded using a fluxgate magnetometer of 70 pT/$\sqrt{\mathrm{Hz}}$ sensitivity. We identified significant differences in the magnetic signatures. In particular, we noticed that Berkeley reaches a near-zero magnetic field activity at night whereas magnetic activity in Brooklyn continues during nighttime. We also present auxiliary measurements acquired using magnetoresistive vector magnetometers (VMR), with sensitivity of 300 pT/$\sqrt{\mathrm{Hz}}$, and demonstrate how cross-correlation, and frequency-domain analysis, combined with data filtering can be used to extract urban magnetometry signals and study local anthropogenic activities. Finally, we discuss the potential of using magnetometer networks to characterize the global magnetic field of cities and give directions for future development.

Rapid parameter estimation of discrete decaying signals using autoencoder networks

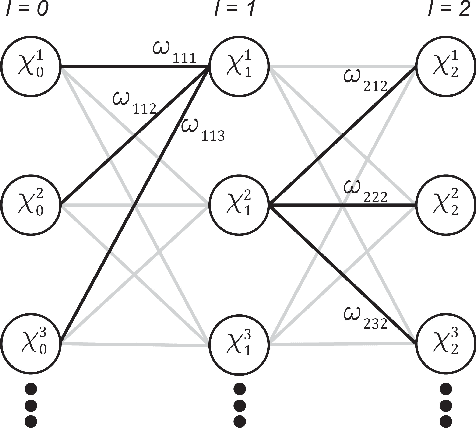
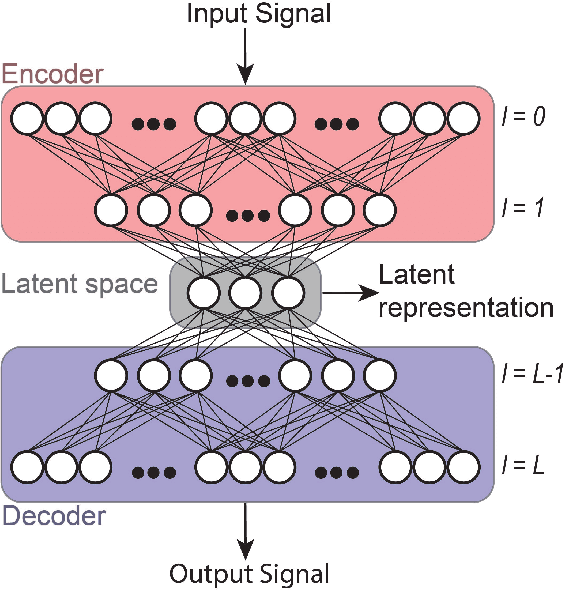
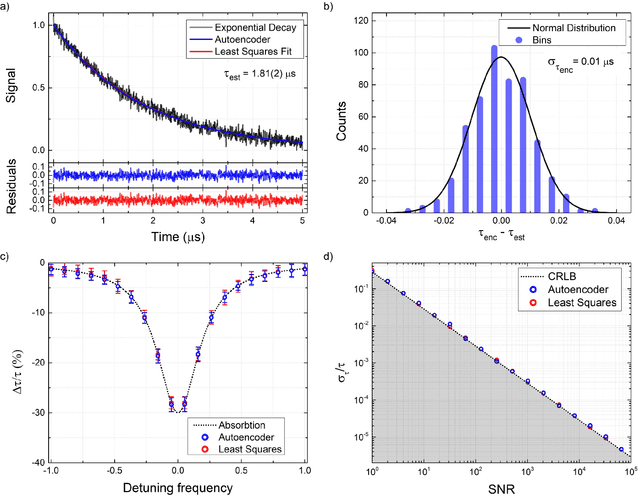
In this work we demonstrate the use of autoencoder networks for rapid extraction of the signal parameters of discretely sampled signals. In particular, we use dense autoencoder networks to extract the parameters of interest from exponentially decaying signals and decaying oscillations. Using a three-stage training method and careful choice of the neural network size, we are able to retrieve the relevant signal parameters directly from the latent space of the autoencoder network at significantly improved rates compared to traditional algorithmic signal-analysis approaches. We show that the achievable precision and accuracy of this method of analysis is similar to conventional, algorithm-based signal analysis methods, by demonstrating that, the extracted signal parameters are approaching their fundamental parameter estimation limit as provided by the Cram\'er-Rao lower bound. Furthermore, we demonstrate that autoencoder networks are able to achieve signal analysis, and, hence, parameter extraction, at rates of 75 kHz, orders-of-magnitude faster than conventional techniques with equal precision. Finally, we explore the limitations of our approach, demonstrating that analysis rates of $>$200 kHz are feasible with further optimization of the transfer rate between the data-acquisition system and data-analysis system.

Deep Neural Networks to Recover Unknown Physical Parameters from Oscillating Time Series

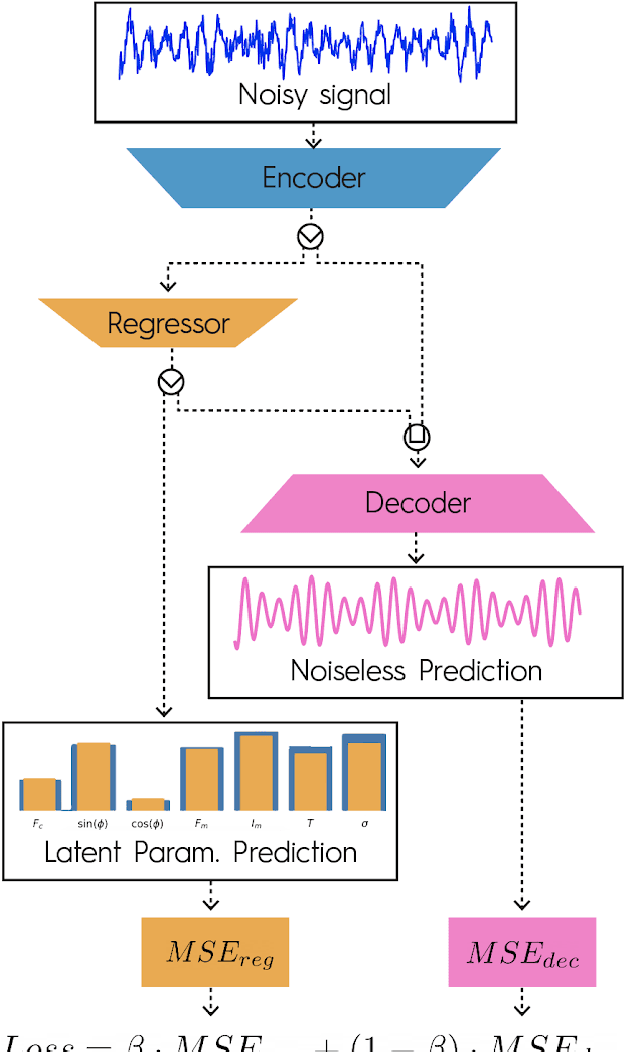
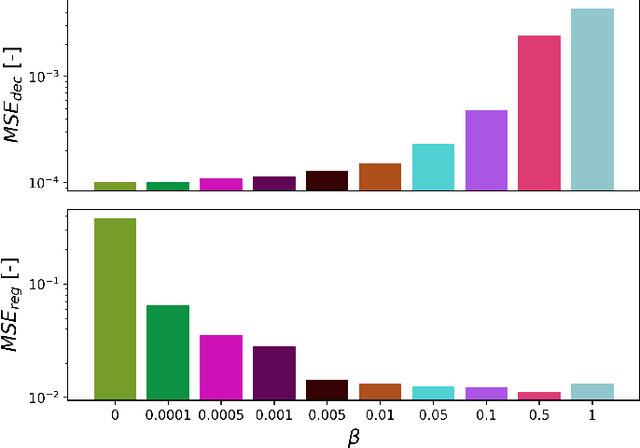
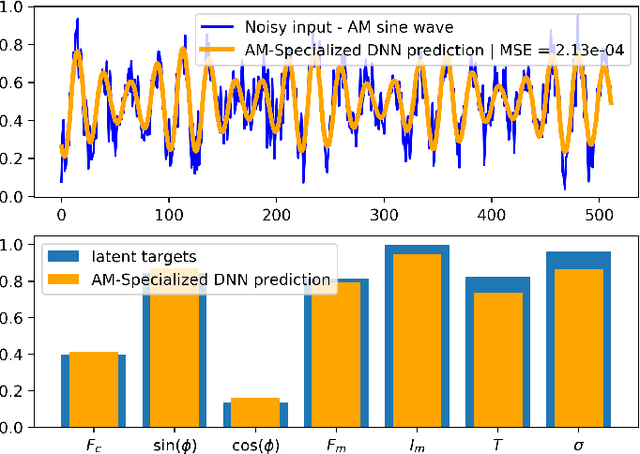
Deep neural networks (DNNs) are widely used in pattern-recognition tasks for which a human comprehensible, quantitative description of the data-generating process, e.g., in the form of equations, cannot be achieved. While doing so, DNNs often produce an abstract (entangled and non-interpretable) representation of the data-generating process. This is one of the reasons why DNNs are not extensively used in physics-signal processing: physicists generally require their analyses to yield quantitative information about the studied systems. In this article we use DNNs to disentangle components of oscillating time series, and recover meaningful information. We show that, because DNNs can find useful abstract feature representations, they can be used when prior knowledge about the signal-generating process exists, but is not complete, as it is particularly the case in "new-physics" searches. To this aim, we train our DNN on synthetic oscillating time series to perform two tasks: a regression of the signal latent parameters and signal denoising by an Autoencoder-like architecture. We show that the regression and denoising performance is similar to those of least-square curve fittings (LS-fit) with true latent parameters' initial guesses, in spite of the DNN needing no initial guesses at all. We then explore applications in which we believe our architecture could prove useful for time-series processing in physics, when prior knowledge is incomplete. As an example, we employ DNNs as a tool to inform LS-fits when initial guesses are unknown. We show that the regression can be performed on some latent parameters, while ignoring the existence of others. Because the Autoencoder needs no prior information about the physical model, the remaining unknown latent parameters can still be captured, thus making use of partial prior knowledge, while leaving space for data exploration and discoveries.