Integrating Inverse and Forward Modeling for Sparse Temporal Data from Sensor Networks

We present CavePerception, a framework for the analysis of sparse data from sensor networks that incorporates elements of inverse modeling and forward modeling. By integrating machine learning with physical modeling in a hypotheses space, we aim to improve the interpretability of sparse, noisy, and potentially incomplete sensor data. The framework assumes data from a two-dimensional sensor network laid out in a graph structure that detects certain objects, with certain motion patterns. Examples of such sensors are magnetometers. Given knowledge about the objects and the way they act on the sensors, one can develop a data generator that produces data from simulated motions of the objects across the sensor field. The framework uses the simulated data to infer object behaviors across the sensor network. The approach is experimentally tested on real-world data, where magnetometers are used on an airport to detect and identify aircraft motions. Experiments demonstrate the value of integrating inverse and forward modeling, enabling intelligent systems to better understand and predict complex, sensor-driven events.

Deep Neural Networks to Recover Unknown Physical Parameters from Oscillating Time Series

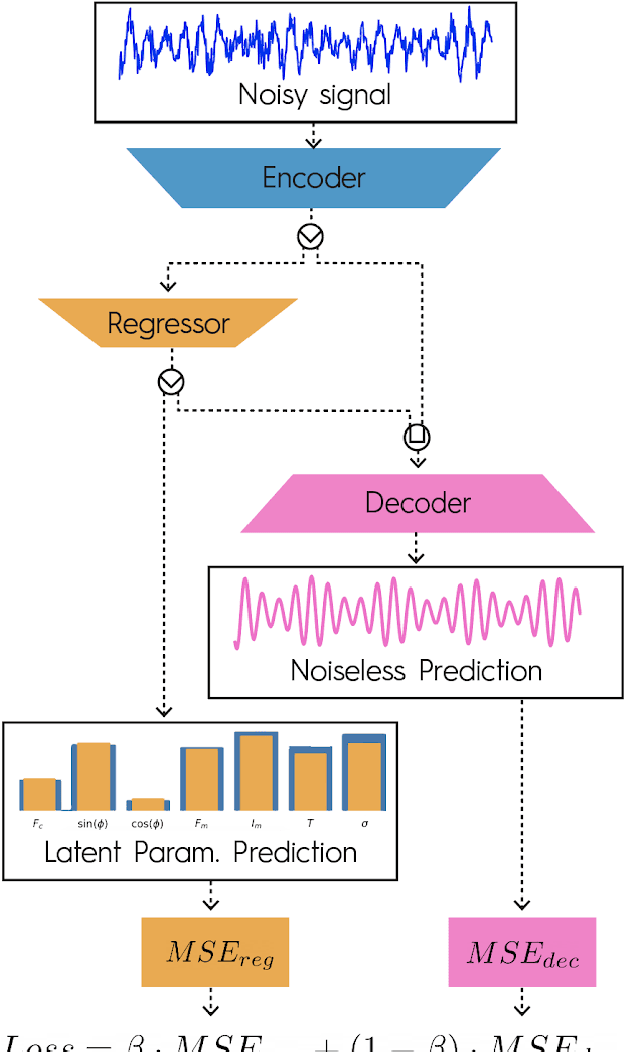
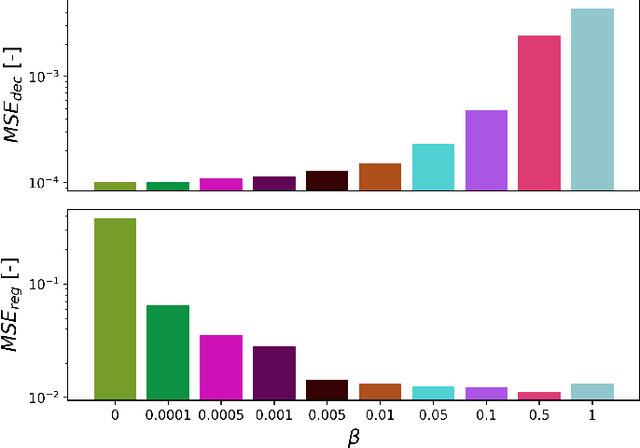
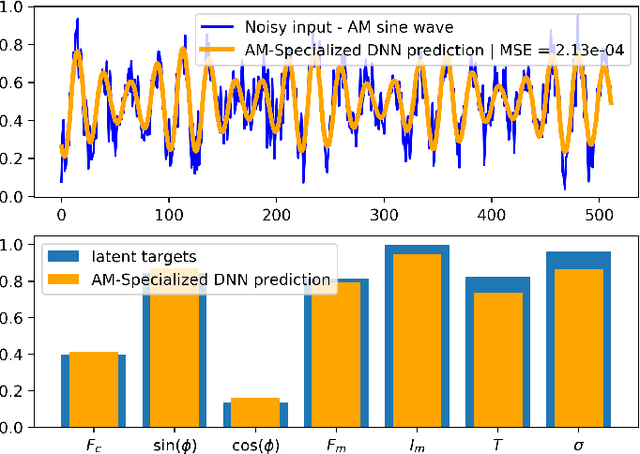
Deep neural networks (DNNs) are widely used in pattern-recognition tasks for which a human comprehensible, quantitative description of the data-generating process, e.g., in the form of equations, cannot be achieved. While doing so, DNNs often produce an abstract (entangled and non-interpretable) representation of the data-generating process. This is one of the reasons why DNNs are not extensively used in physics-signal processing: physicists generally require their analyses to yield quantitative information about the studied systems. In this article we use DNNs to disentangle components of oscillating time series, and recover meaningful information. We show that, because DNNs can find useful abstract feature representations, they can be used when prior knowledge about the signal-generating process exists, but is not complete, as it is particularly the case in "new-physics" searches. To this aim, we train our DNN on synthetic oscillating time series to perform two tasks: a regression of the signal latent parameters and signal denoising by an Autoencoder-like architecture. We show that the regression and denoising performance is similar to those of least-square curve fittings (LS-fit) with true latent parameters' initial guesses, in spite of the DNN needing no initial guesses at all. We then explore applications in which we believe our architecture could prove useful for time-series processing in physics, when prior knowledge is incomplete. As an example, we employ DNNs as a tool to inform LS-fits when initial guesses are unknown. We show that the regression can be performed on some latent parameters, while ignoring the existence of others. Because the Autoencoder needs no prior information about the physical model, the remaining unknown latent parameters can still be captured, thus making use of partial prior knowledge, while leaving space for data exploration and discoveries.