A Surprisingly Simple Continuous-Action POMDP Solver: Lazy Cross-Entropy Search Over Policy Trees

The Partially Observable Markov Decision Process (POMDP) provides a principled framework for decision making in stochastic partially observable environments. However, computing good solutions for problems with continuous action spaces remains challenging. To ease this challenge, we propose a simple online POMDP solver, called Lazy Cross-Entropy Search Over Policy Trees (LCEOPT). At each planning step, our method uses a lazy Cross-Entropy method to search the space of policy trees, which provide a simple policy representation. Specifically, we maintain a distribution on promising finite-horizon policy trees. The distribution is iteratively updated by sampling policies, evaluating them via Monte Carlo simulation, and refitting them to the top-performing ones. Our method is lazy in the sense that it exploits the policy tree representation to avoid redundant computations in policy sampling, evaluation, and distribution update. This leads to computational savings of up to two orders of magnitude. Our LCEOPT is surprisingly simple as compared to existing state-of-the-art methods, yet empirically outperforms them on several continuous-action POMDP problems, particularly for problems with higher-dimensional action spaces.

A Flow-Based Generative Model for Rare-Event Simulation

Solving decision problems in complex, stochastic environments is often achieved by estimating the expected outcome of decisions via Monte Carlo sampling. However, sampling may overlook rare, but important events, which can severely impact the decision making process. We present a method in which a Normalizing Flow generative model is trained to simulate samples directly from a conditional distribution given that a rare event occurs. By utilizing Coupling Flows, our model can, in principle, approximate any sampling distribution arbitrarily well. By combining the approximation method with Importance Sampling, highly accurate estimates of complicated integrals and expectations can be obtained. We include several examples to demonstrate how the method can be used for efficient sampling and estimation, even in high-dimensional and rare-event settings. We illustrate that by simulating directly from a rare-event distribution significant insight can be gained into the way rare events happen.

Adaptive Discretization using Voronoi Trees for Continuous POMDPs

Solving continuous Partially Observable Markov Decision Processes (POMDPs) is challenging, particularly for high-dimensional continuous action spaces. To alleviate this difficulty, we propose a new sampling-based online POMDP solver, called Adaptive Discretization using Voronoi Trees (ADVT). It uses Monte Carlo Tree Search in combination with an adaptive discretization of the action space as well as optimistic optimization to efficiently sample high-dimensional continuous action spaces and compute the best action to perform. Specifically, we adaptively discretize the action space for each sampled belief using a hierarchical partition called Voronoi tree, which is a Binary Space Partitioning that implicitly maintains the partition of a cell as the Voronoi diagram of two points sampled from the cell. ADVT uses the estimated diameters of the cells to form an upper-confidence bound on the action value function within the cell, guiding the Monte Carlo Tree Search expansion and further discretization of the action space. This enables ADVT to better exploit local information with respect to the action value function, allowing faster identification of the most promising regions in the action space, compared to existing solvers. Voronoi trees keep the cost of partitioning and estimating the diameter of each cell low, even in high-dimensional spaces where many sampled points are required to cover the space well. ADVT additionally handles continuous observation spaces, by adopting an observation progressive widening strategy, along with a weighted particle representation of beliefs. Experimental results indicate that ADVT scales substantially better to high-dimensional continuous action spaces, compared to state-of-the-art methods.

Adaptive Discretization using Voronoi Trees for Continuous-Action POMDPs

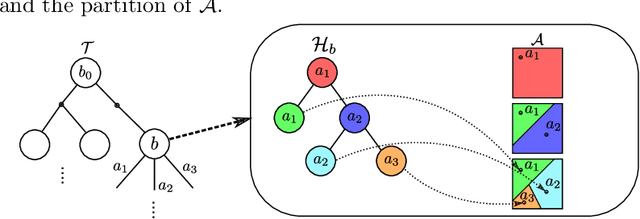
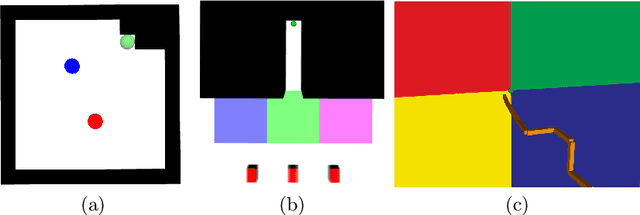
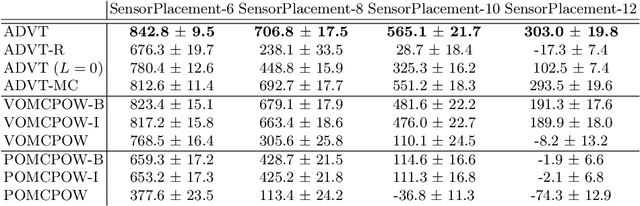
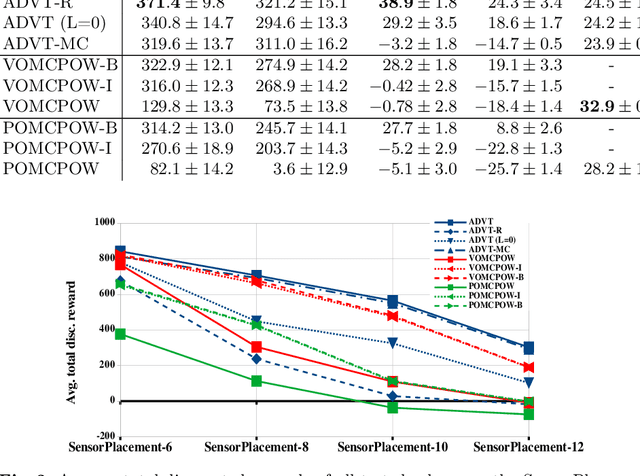
Solving Partially Observable Markov Decision Processes (POMDPs) with continuous actions is challenging, particularly for high-dimensional action spaces. To alleviate this difficulty, we propose a new sampling-based online POMDP solver, called Adaptive Discretization using Voronoi Trees (ADVT). It uses Monte Carlo Tree Search in combination with an adaptive discretization of the action space as well as optimistic optimization to efficiently sample high-dimensional continuous action spaces and compute the best action to perform. Specifically, we adaptively discretize the action space for each sampled belief using a hierarchical partition which we call a Voronoi tree. A Voronoi tree is a Binary Space Partitioning (BSP) that implicitly maintains the partition of a cell as the Voronoi diagram of two points sampled from the cell. This partitioning strategy keeps the cost of partitioning and estimating the size of each cell low, even in high-dimensional spaces where many sampled points are required to cover the space well. ADVT uses the estimated sizes of the cells to form an upper-confidence bound of the action values of the cell, and in turn uses the upper-confidence bound to guide the Monte Carlo Tree Search expansion and further discretization of the action space. This strategy enables ADVT to better exploit local information in the action space, leading to an action space discretization that is more adaptive, and hence more efficient in computing good POMDP solutions, compared to existing solvers. Experiments on simulations of four types of benchmark problems indicate that ADVT outperforms and scales substantially better to high-dimensional continuous action spaces, compared to state-of-the-art continuous action POMDP solvers.