Adaptive Discretization using Voronoi Trees for Continuous-Action POMDPs
Paper and Code
Sep 13, 2022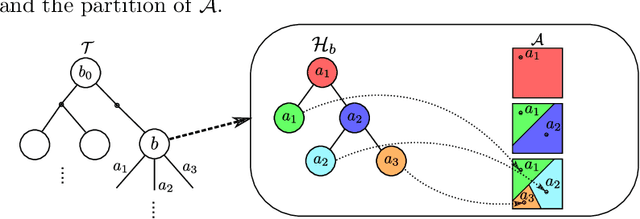
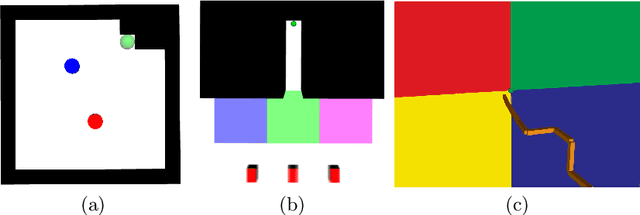
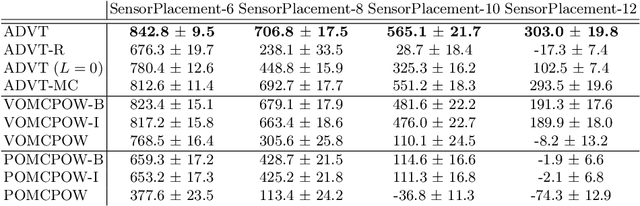
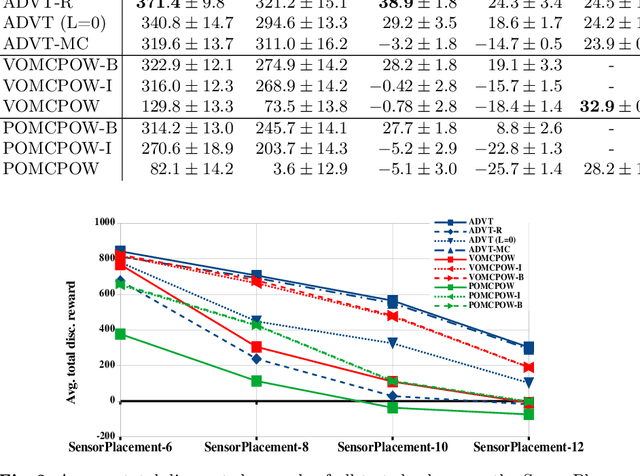
Solving Partially Observable Markov Decision Processes (POMDPs) with continuous actions is challenging, particularly for high-dimensional action spaces. To alleviate this difficulty, we propose a new sampling-based online POMDP solver, called Adaptive Discretization using Voronoi Trees (ADVT). It uses Monte Carlo Tree Search in combination with an adaptive discretization of the action space as well as optimistic optimization to efficiently sample high-dimensional continuous action spaces and compute the best action to perform. Specifically, we adaptively discretize the action space for each sampled belief using a hierarchical partition which we call a Voronoi tree. A Voronoi tree is a Binary Space Partitioning (BSP) that implicitly maintains the partition of a cell as the Voronoi diagram of two points sampled from the cell. This partitioning strategy keeps the cost of partitioning and estimating the size of each cell low, even in high-dimensional spaces where many sampled points are required to cover the space well. ADVT uses the estimated sizes of the cells to form an upper-confidence bound of the action values of the cell, and in turn uses the upper-confidence bound to guide the Monte Carlo Tree Search expansion and further discretization of the action space. This strategy enables ADVT to better exploit local information in the action space, leading to an action space discretization that is more adaptive, and hence more efficient in computing good POMDP solutions, compared to existing solvers. Experiments on simulations of four types of benchmark problems indicate that ADVT outperforms and scales substantially better to high-dimensional continuous action spaces, compared to state-of-the-art continuous action POMDP solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge