Provably Feedback-Efficient Reinforcement Learning via Active Reward Learning

An appropriate reward function is of paramount importance in specifying a task in reinforcement learning (RL). Yet, it is known to be extremely challenging in practice to design a correct reward function for even simple tasks. Human-in-the-loop (HiL) RL allows humans to communicate complex goals to the RL agent by providing various types of feedback. However, despite achieving great empirical successes, HiL RL usually requires too much feedback from a human teacher and also suffers from insufficient theoretical understanding. In this paper, we focus on addressing this issue from a theoretical perspective, aiming to provide provably feedback-efficient algorithmic frameworks that take human-in-the-loop to specify rewards of given tasks. We provide an active-learning-based RL algorithm that first explores the environment without specifying a reward function and then asks a human teacher for only a few queries about the rewards of a task at some state-action pairs. After that, the algorithm guarantees to provide a nearly optimal policy for the task with high probability. We show that, even with the presence of random noise in the feedback, the algorithm only takes $\widetilde{O}(H{{\dim_{R}^2}})$ queries on the reward function to provide an $\epsilon$-optimal policy for any $\epsilon > 0$. Here $H$ is the horizon of the RL environment, and $\dim_{R}$ specifies the complexity of the function class representing the reward function. In contrast, standard RL algorithms require to query the reward function for at least $\Omega(\operatorname{poly}(d, 1/\epsilon))$ state-action pairs where $d$ depends on the complexity of the environmental transition.

Learning Rationalizable Equilibria in Multiplayer Games

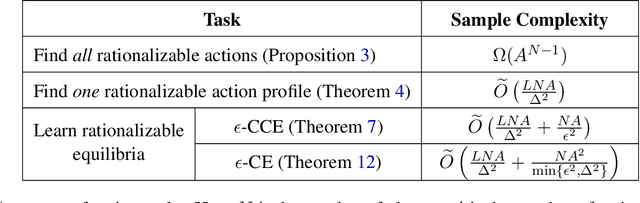
A natural goal in multiagent learning besides finding equilibria is to learn rationalizable behavior, where players learn to avoid iteratively dominated actions. However, even in the basic setting of multiplayer general-sum games, existing algorithms require a number of samples exponential in the number of players to learn rationalizable equilibria under bandit feedback. This paper develops the first line of efficient algorithms for learning rationalizable Coarse Correlated Equilibria (CCE) and Correlated Equilibria (CE) whose sample complexities are polynomial in all problem parameters including the number of players. To achieve this result, we also develop a new efficient algorithm for the simpler task of finding one rationalizable action profile (not necessarily an equilibrium), whose sample complexity substantially improves over the best existing results of Wu et al. (2021). Our algorithms incorporate several novel techniques to guarantee rationalizability and no (swap-)regret simultaneously, including a correlated exploration scheme and adaptive learning rates, which may be of independent interest. We complement our results with a sample complexity lower bound showing the sharpness of our guarantees.

Online Sub-Sampling for Reinforcement Learning with General Function Approximation

Designing provably efficient algorithms with general function approximation is an important open problem in reinforcement learning. Recently, Wang et al.~[2020c] establish a value-based algorithm with general function approximation that enjoys $\widetilde{O}(\mathrm{poly}(dH)\sqrt{K})$\footnote{Throughout the paper, we use $\widetilde{O}(\cdot)$ to suppress logarithm factors. } regret bound, where $d$ depends on the complexity of the function class, $H$ is the planning horizon, and $K$ is the total number of episodes. However, their algorithm requires $\Omega(K)$ computation time per round, rendering the algorithm inefficient for practical use. In this paper, by applying online sub-sampling techniques, we develop an algorithm that takes $\widetilde{O}(\mathrm{poly}(dH))$ computation time per round on average, and enjoys nearly the same regret bound. Furthermore, the algorithm achieves low switching cost, i.e., it changes the policy only $\widetilde{O}(\mathrm{poly}(dH))$ times during its execution, making it appealing to be implemented in real-life scenarios. Moreover, by using an upper-confidence based exploration-driven reward function, the algorithm provably explores the environment in the reward-free setting. In particular, after $\widetilde{O}(\mathrm{poly}(dH))/\epsilon^2$ rounds of exploration, the algorithm outputs an $\epsilon$-optimal policy for any given reward function.