Learning Rationalizable Equilibria in Multiplayer Games
Paper and Code
Oct 20, 2022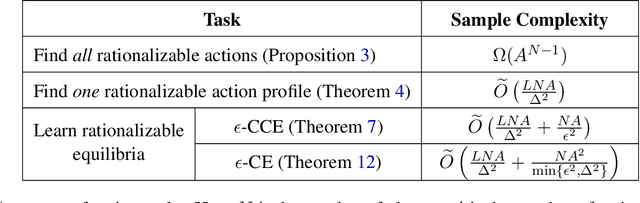
A natural goal in multiagent learning besides finding equilibria is to learn rationalizable behavior, where players learn to avoid iteratively dominated actions. However, even in the basic setting of multiplayer general-sum games, existing algorithms require a number of samples exponential in the number of players to learn rationalizable equilibria under bandit feedback. This paper develops the first line of efficient algorithms for learning rationalizable Coarse Correlated Equilibria (CCE) and Correlated Equilibria (CE) whose sample complexities are polynomial in all problem parameters including the number of players. To achieve this result, we also develop a new efficient algorithm for the simpler task of finding one rationalizable action profile (not necessarily an equilibrium), whose sample complexity substantially improves over the best existing results of Wu et al. (2021). Our algorithms incorporate several novel techniques to guarantee rationalizability and no (swap-)regret simultaneously, including a correlated exploration scheme and adaptive learning rates, which may be of independent interest. We complement our results with a sample complexity lower bound showing the sharpness of our guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge