GoRINNs: Godunov-Riemann Informed Neural Networks for Learning Hyperbolic Conservation Laws

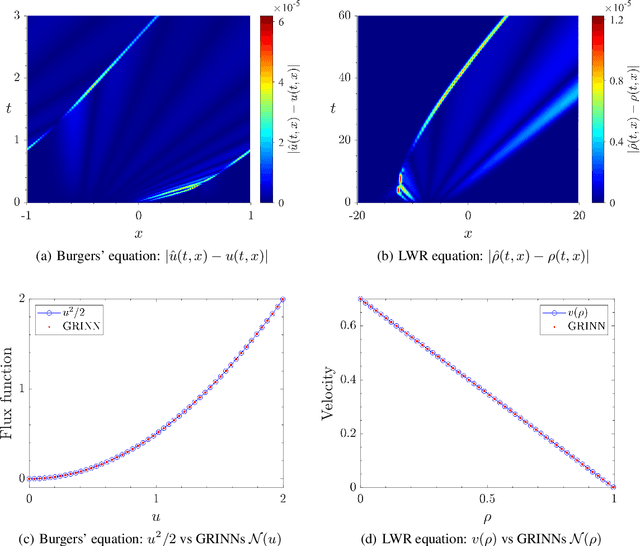
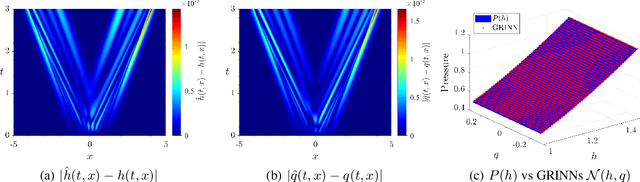
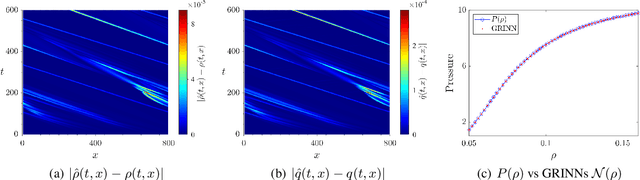
We present GoRINNs: numerical analysis-informed neural networks for the solution of inverse problems of non-linear systems of conservation laws. GoRINNs are based on high-resolution Godunov schemes for the solution of the Riemann problem in hyperbolic Partial Differential Equations (PDEs). In contrast to other existing machine learning methods that learn the numerical fluxes of conservative Finite Volume methods, GoRINNs learn the physical flux function per se. Due to their structure, GoRINNs provide interpretable, conservative schemes, that learn the solution operator on the basis of approximate Riemann solvers that satisfy the Rankine-Hugoniot condition. The performance of GoRINNs is assessed via four benchmark problems, namely the Burgers', the Shallow Water, the Lighthill-Whitham-Richards and the Payne-Whitham traffic flow models. The solution profiles of these PDEs exhibit shock waves, rarefactions and/or contact discontinuities at finite times. We demonstrate that GoRINNs provide a very high accuracy both in the smooth and discontinuous regions.

GRINNs: Godunov-Riemann Informed Neural Networks for Learning Hyperbolic Conservation Laws

We present GRINNs: numerical analysis-informed neural networks for the solution of inverse problems of non-linear systems of conservation laws. GRINNs are based on high-resolution Godunov schemes for the solution of the Riemann problem in hyperbolic Partial Differential Equations (PDEs). In contrast to other existing machine learning methods that learn the numerical fluxes of conservative Finite Volume methods, GRINNs learn the physical flux function per se. Due to their structure, GRINNs provide interpretable, conservative schemes, that learn the solution operator on the basis of approximate Riemann solvers that satisfy the Rankine-Hugoniot condition. The performance of GRINNs is assessed via four benchmark problems, namely the Burgers', the Shallow Water, the Lighthill-Whitham-Richards and the Payne-Whitham traffic flow models. The solution profiles of these PDEs exhibit shock waves, rarefactions and/or contact discontinuities at finite times. We demonstrate that GRINNs provide a very high accuracy both in the smooth and discontinuous regions.

A physics-informed neural network method for the approximation of slow invariant manifolds for the general class of stiff systems of ODEs

We present a physics-informed neural network (PINN) approach for the discovery of slow invariant manifolds (SIMs), for the most general class of fast/slow dynamical systems of ODEs. In contrast to other machine learning (ML) approaches that construct reduced order black box surrogate models using simple regression, and/or require a priori knowledge of the fast and slow variables, our approach, simultaneously decomposes the vector field into fast and slow components and provides a functional of the underlying SIM in a closed form. The decomposition is achieved by finding a transformation of the state variables to the fast and slow ones, which enables the derivation of an explicit, in terms of fast variables, SIM functional. The latter is obtained by solving a PDE corresponding to the invariance equation within the Geometric Singular Perturbation Theory (GSPT) using a single-layer feedforward neural network with symbolic differentiation. The performance of the proposed physics-informed ML framework is assessed via three benchmark problems: the Michaelis-Menten, the target mediated drug disposition (TMDD) reaction model and a fully competitive substrate-inhibitor(fCSI) mechanism. We also provide a comparison with other GPST methods, namely the quasi steady state approximation (QSSA), the partial equilibrium approximation (PEA) and CSP with one and two iterations. We show that the proposed PINN scheme provides SIM approximations, of equivalent or even higher accuracy, than those provided by QSSA, PEA and CSP, especially close to the boundaries of the underlying SIMs.

Slow Invariant Manifolds of Singularly Perturbed Systems via Physics-Informed Machine Learning

We present a physics-informed machine-learning (PIML) approach for the approximation of slow invariant manifolds (SIMs) of singularly perturbed systems, providing functionals in an explicit form that facilitate the construction and numerical integration of reduced order models (ROMs). The proposed scheme solves a partial differential equation corresponding to the invariance equation (IE) within the Geometric Singular Perturbation Theory (GSPT) framework. For the solution of the IE, we used two neural network structures, namely feedforward neural networks (FNNs), and random projection neural networks (RPNNs), with symbolic differentiation for the computation of the gradients required for the learning process. The efficiency of our PIML method is assessed via three benchmark problems, namely the Michaelis-Menten, the target mediated drug disposition reaction mechanism, and the 3D Sel'kov model. We show that the proposed PIML scheme provides approximations, of equivalent or even higher accuracy, than those provided by other traditional GSPT-based methods, and importantly, for any practical purposes, it is not affected by the magnitude of the perturbation parameter. This is of particular importance, as there are many systems for which the gap between the fast and slow timescales is not that big, but still ROMs can be constructed. A comparison of the computational costs between symbolic, automatic and numerical approximation of the required derivatives in the learning process is also provided.

Data-driven Control of Agent-based Models: an Equation/Variable-free Machine Learning Approach

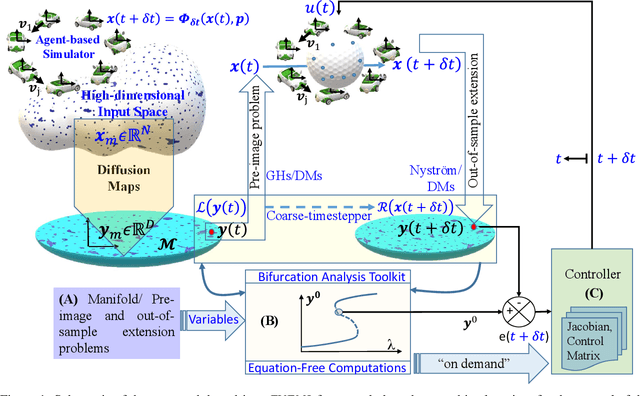
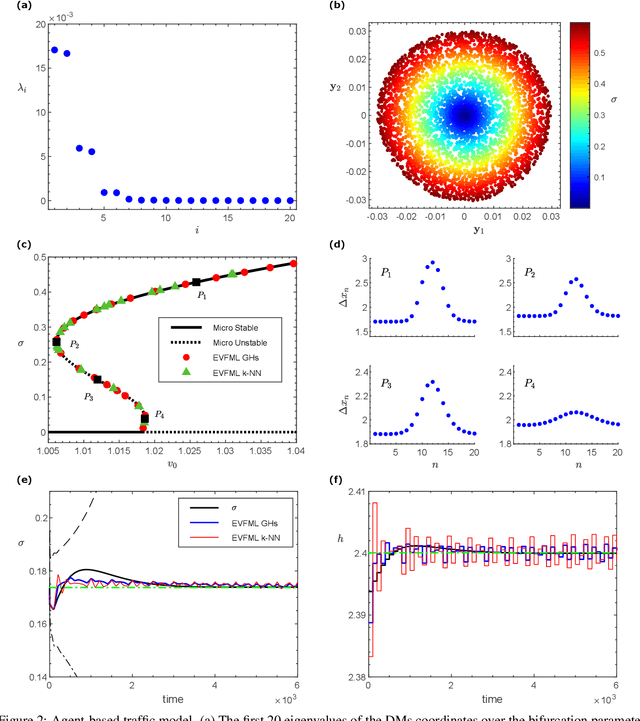
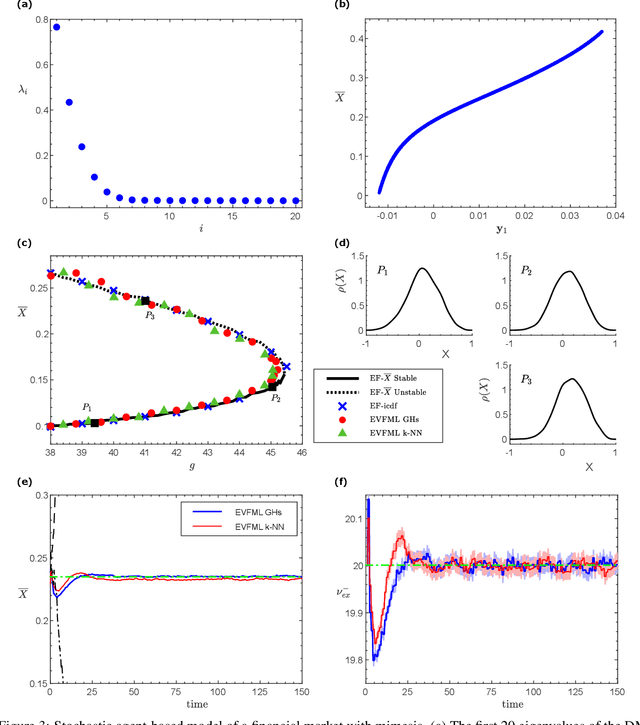
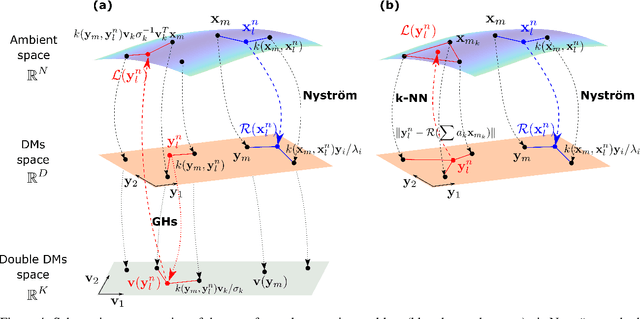
We present an Equation/Variable free machine learning (EVFML) framework for the control of the collective dynamics of complex/multiscale systems modelled via microscopic/agent-based simulators. The approach obviates the need for construction of surrogate, reduced-order models.~The proposed implementation consists of three steps: (A) from high-dimensional agent-based simulations, machine learning (in particular, non-linear manifold learning (Diffusion Maps (DMs)) helps identify a set of coarse-grained variables that parametrize the low-dimensional manifold on which the emergent/collective dynamics evolve. The out-of-sample extension and pre-image problems, i.e. the construction of non-linear mappings from the high-dimensional input space to the low-dimensional manifold and back, are solved by coupling DMs with the Nystrom extension and Geometric Harmonics, respectively; (B) having identified the manifold and its coordinates, we exploit the Equation-free approach to perform numerical bifurcation analysis of the emergent dynamics; then (C) based on the previous steps, we design data-driven embedded wash-out controllers that drive the agent-based simulators to their intrinsic, imprecisely known, emergent open-loop unstable steady-states, thus demonstrating that the scheme is robust against numerical approximation errors and modelling uncertainty.~The efficiency of the framework is illustrated by controlling emergent unstable (i) traveling waves of a deterministic agent-based model of traffic dynamics, and (ii) equilibria of a stochastic financial market agent model with mimesis.