GoRINNs: Godunov-Riemann Informed Neural Networks for Learning Hyperbolic Conservation Laws
Paper and Code
Oct 31, 2024
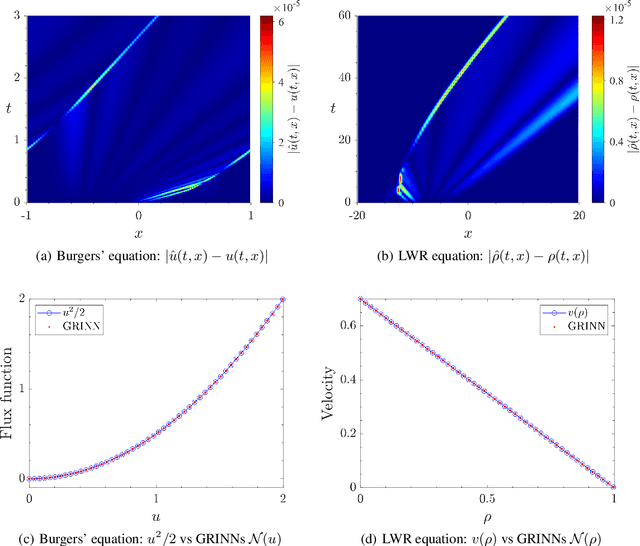
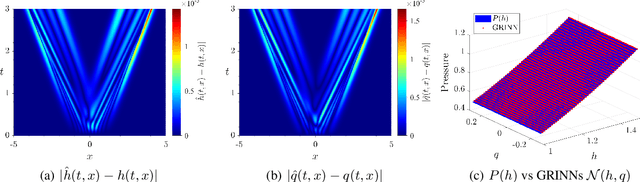
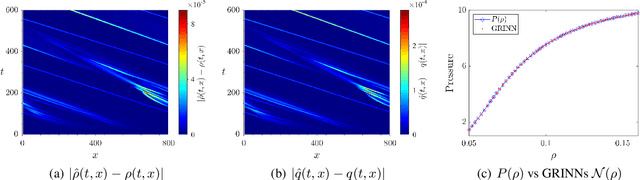
We present GoRINNs: numerical analysis-informed neural networks for the solution of inverse problems of non-linear systems of conservation laws. GoRINNs are based on high-resolution Godunov schemes for the solution of the Riemann problem in hyperbolic Partial Differential Equations (PDEs). In contrast to other existing machine learning methods that learn the numerical fluxes of conservative Finite Volume methods, GoRINNs learn the physical flux function per se. Due to their structure, GoRINNs provide interpretable, conservative schemes, that learn the solution operator on the basis of approximate Riemann solvers that satisfy the Rankine-Hugoniot condition. The performance of GoRINNs is assessed via four benchmark problems, namely the Burgers', the Shallow Water, the Lighthill-Whitham-Richards and the Payne-Whitham traffic flow models. The solution profiles of these PDEs exhibit shock waves, rarefactions and/or contact discontinuities at finite times. We demonstrate that GoRINNs provide a very high accuracy both in the smooth and discontinuous regions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge