SINR: Sparsity Driven Compressed Implicit Neural Representations

Implicit Neural Representations (INRs) are increasingly recognized as a versatile data modality for representing discretized signals, offering benefits such as infinite query resolution and reduced storage requirements. Existing signal compression approaches for INRs typically employ one of two strategies: 1. direct quantization with entropy coding of the trained INR; 2. deriving a latent code on top of the INR through a learnable transformation. Thus, their performance is heavily dependent on the quantization and entropy coding schemes employed. In this paper, we introduce SINR, an innovative compression algorithm that leverages the patterns in the vector spaces formed by weights of INRs. We compress these vector spaces using a high-dimensional sparse code within a dictionary. Further analysis reveals that the atoms of the dictionary used to generate the sparse code do not need to be learned or transmitted to successfully recover the INR weights. We demonstrate that the proposed approach can be integrated with any existing INR-based signal compression technique. Our results indicate that SINR achieves substantial reductions in storage requirements for INRs across various configurations, outperforming conventional INR-based compression baselines. Furthermore, SINR maintains high-quality decoding across diverse data modalities, including images, occupancy fields, and Neural Radiance Fields.

GAUSS: Guided Encoder-Decoder Architecture for Hyperspectral Unmixing with Spatial Smoothness

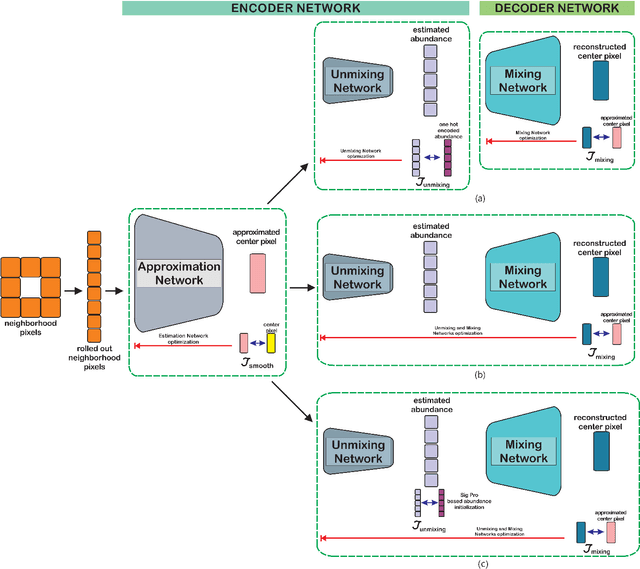
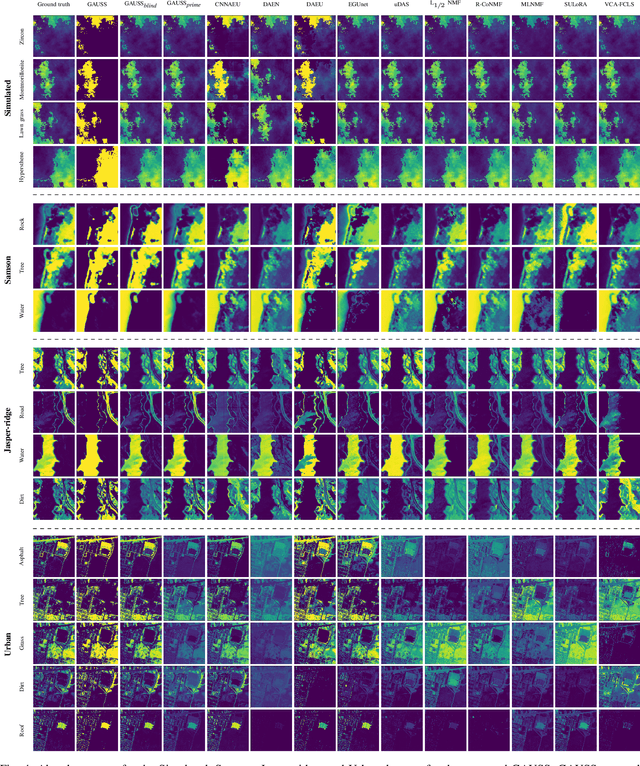
In recent hyperspectral unmixing (HU) literature, the application of deep learning (DL) has become more prominent, especially with the autoencoder (AE) architecture. We propose a split architecture and use a pseudo-ground truth for abundances to guide the `unmixing network' (UN) optimization. Preceding the UN, an `approximation network' (AN) is proposed, which will improve the association between the centre pixel and its neighbourhood. Hence, it will accentuate spatial correlation in the abundances as its output is the input to the UN and the reference for the `mixing network' (MN). In the Guided Encoder-Decoder Architecture for Hyperspectral Unmixing with Spatial Smoothness (GAUSS), we proposed using one-hot encoded abundances as the pseudo-ground truth to guide the UN; computed using the k-means algorithm to exclude the use of prior HU methods. Furthermore, we release the single-layer constraint on MN by introducing the UN generated abundances in contrast to the standard AE for HU. Secondly, we experimented with two modifications on the pre-trained network using the GAUSS method. In GAUSS$_\textit{blind}$, we have concatenated the UN and the MN to back-propagate the reconstruction error gradients to the encoder. Then, in the GAUSS$_\textit{prime}$, abundance results of a signal processing (SP) method with reliable abundance results were used as the pseudo-ground truth with the GAUSS architecture. According to quantitative and graphical results for four experimental datasets, the three architectures either transcended or equated the performance of existing HU algorithms from both DL and SP domains.