A Little Confidence Goes a Long Way

We introduce a group of related methods for binary classification tasks using probes of the hidden state activations in large language models (LLMs). Performance is on par with the largest and most advanced LLMs currently available, but requiring orders of magnitude fewer computational resources and not requiring labeled data. This approach involves translating class labels into a semantically rich description, spontaneous symmetry breaking of multilayer perceptron probes for unsupervised learning and inference, training probes to generate confidence scores (prior probabilities) from hidden state activations subject to known constraints via entropy maximization, and selecting the most confident probe model from an ensemble for prediction. These techniques are evaluated on four datasets using five base LLMs.

Can't Remember Details in Long Documents? You Need Some R&R

Long-context large language models (LLMs) hold promise for tasks such as question-answering (QA) over long documents, but they tend to miss important information in the middle of context documents (arXiv:2307.03172v3). Here, we introduce $\textit{R&R}$ -- a combination of two novel prompt-based methods called $\textit{reprompting}$ and $\textit{in-context retrieval}$ (ICR) -- to alleviate this effect in document-based QA. In reprompting, we repeat the prompt instructions periodically throughout the context document to remind the LLM of its original task. In ICR, rather than instructing the LLM to answer the question directly, we instruct it to retrieve the top $k$ passage numbers most relevant to the given question, which are then used as an abbreviated context in a second QA prompt. We test R&R with GPT-4 Turbo and Claude-2.1 on documents up to 80k tokens in length and observe a 16-point boost in QA accuracy on average. Our further analysis suggests that R&R improves performance on long document-based QA because it reduces the distance between relevant context and the instructions. Finally, we show that compared to short-context chunkwise methods, R&R enables the use of larger chunks that cost fewer LLM calls and output tokens, while minimizing the drop in accuracy.

Densely Connected $G$-invariant Deep Neural Networks with Signed Permutation Representations

We introduce and investigate, for finite groups $G$, $G$-invariant deep neural network ($G$-DNN) architectures with ReLU activation that are densely connected -- i.e., include all possible skip connections. In contrast to other $G$-invariant architectures in the literature, the preactivations of the$G$-DNNs presented here are able to transform by \emph{signed} permutation representations (signed perm-reps) of $G$. Moreover, the individual layers of the $G$-DNNs are not required to be $G$-equivariant; instead, the preactivations are constrained to be $G$-equivariant functions of the network input in a way that couples weights across all layers. The result is a richer family of $G$-invariant architectures never seen previously. We derive an efficient implementation of $G$-DNNs after a reparameterization of weights, as well as necessary and sufficient conditions for an architecture to be "admissible" -- i.e., nondegenerate and inequivalent to smaller architectures. We include code that allows a user to build a $G$-DNN interactively layer-by-layer, with the final architecture guaranteed to be admissible. Finally, we apply $G$-DNNs to two example problems -- (1) multiplication in $\{-1, 1\}$ (with theoretical guarantees) and (2) 3D object classification -- finding that the inclusion of signed perm-reps significantly boosts predictive performance compared to baselines with only ordinary (i.e., unsigned) perm-reps.

A Classification of $G$-invariant Shallow Neural Networks

When trying to fit a deep neural network (DNN) to a $G$-invariant target function with respect to a group $G$, it only makes sense to constrain the DNN to be $G$-invariant as well. However, there can be many different ways to do this, thus raising the problem of "$G$-invariant neural architecture design": What is the optimal $G$-invariant architecture for a given problem? Before we can consider the optimization problem itself, we must understand the search space, the architectures in it, and how they relate to one another. In this paper, we take a first step towards this goal; we prove a theorem that gives a classification of all $G$-invariant single-hidden-layer or "shallow" neural network ($G$-SNN) architectures with ReLU activation for any finite orthogonal group $G$. The proof is based on a correspondence of every $G$-SNN to a signed permutation representation of $G$ acting on the hidden neurons. The classification is equivalently given in terms of the first cohomology classes of $G$, thus admitting a topological interpretation. Based on a code implementation, we enumerate the $G$-SNN architectures for some example groups $G$ and visualize their structure. We draw the network morphisms between the enumerated architectures that can be leveraged during neural architecture search (NAS). Finally, we prove that architectures corresponding to inequivalent cohomology classes in a given cohomology ring coincide in function space only when their weight matrices are zero, and we discuss the implications of this in the context of NAS.

A Group-Equivariant Autoencoder for Identifying Spontaneously Broken Symmetries in the Ising Model

We introduce the group-equivariant autoencoder (GE-autoencoder) -- a novel deep neural network method that locates phase boundaries in the Ising universality class by determining which symmetries of the Hamiltonian are broken at each temperature. The encoder network of the GE-autoencoder models the order parameter observable associated with the phase transition. The parameters of the GE-autoencoder are constrained such that the encoder is invariant to the subgroup of symmetries that never break; this results in a dramatic reduction in the number of free parameters such that the GE-autoencoder size is independent of the system size. The loss function of the GE-autoencoder includes regularization terms that enforce equivariance to the remaining quotient group of symmetries. We test the GE-autoencoder method on the 2D classical ferromagnetic and antiferromagnetic Ising models, finding that the GE-autoencoder (1) accurately determines which symmetries are broken at each temperature, and (2) estimates the critical temperature with greater accuracy and time-efficiency than a symmetry-agnostic autoencoder, once finite-size scaling analysis is taken into account.

Wide Neural Networks with Bottlenecks are Deep Gaussian Processes

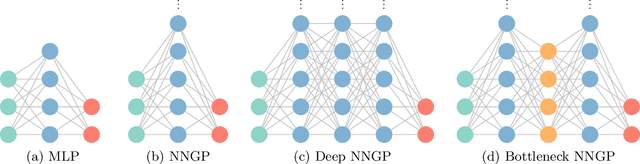
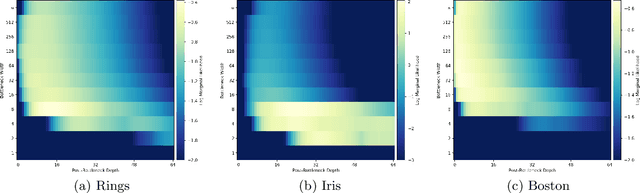
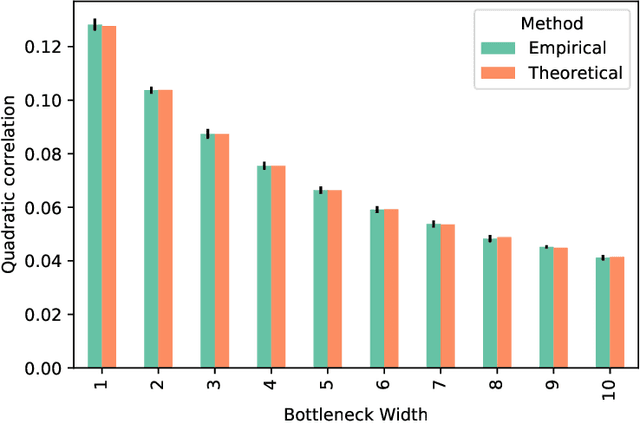
There has recently been much work on the "wide limit" of neural networks, where Bayesian neural networks (BNNs) are shown to converge to a Gaussian process (GP) as all hidden layers are sent to infinite width. However, these results do not apply to architectures that require one or more of the hidden layers to remain narrow. In this paper, we consider the wide limit of BNNs where some hidden layers, called "bottlenecks", are held at finite width. The result is a composition of GPs that we term a "bottleneck neural network Gaussian process" (bottleneck NNGP). Although intuitive, the subtlety of the proof is in showing that the wide limit of a composition of networks is in fact the composition of the limiting GPs. We also analyze theoretically a single-bottleneck NNGP, finding that the bottleneck induces dependence between the outputs of a multi-output network that persists through extreme post-bottleneck depths, and prevents the kernel of the network from losing discriminative power at extreme post-bottleneck depths.