Expansive Synthesis: Generating Large-Scale Datasets from Minimal Samples

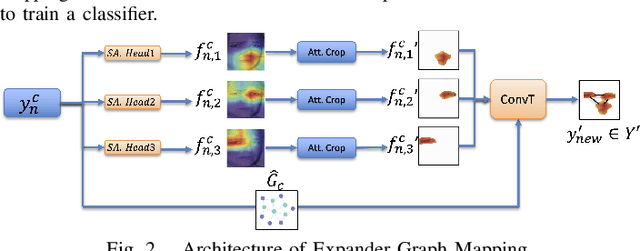
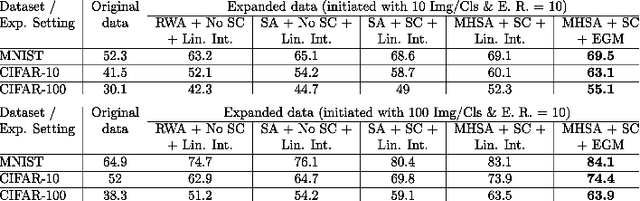
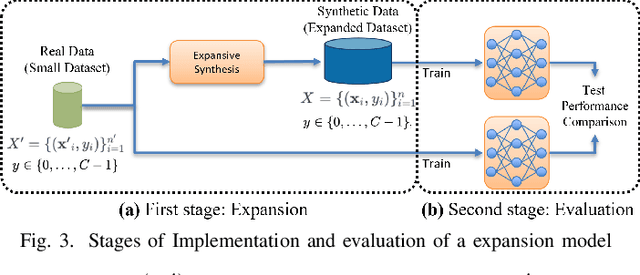
The challenge of limited availability of data for training in machine learning arises in many applications and the impact on performance and generalization is serious. Traditional data augmentation methods aim to enhance training with a moderately sufficient data set. Generative models like Generative Adversarial Networks (GANs) often face problematic convergence when generating significant and diverse data samples. Diffusion models, though effective, still struggle with high computational cost and long training times. This paper introduces an innovative Expansive Synthesis model that generates large-scale, high-fidelity datasets from minimal samples. The proposed approach exploits expander graph mappings and feature interpolation to synthesize expanded datasets while preserving the intrinsic data distribution and feature structural relationships. The rationale of the model is rooted in the non-linear property of neural networks' latent space and in its capture by a Koopman operator to yield a linear space of features to facilitate the construction of larger and enriched consistent datasets starting with a much smaller dataset. This process is optimized by an autoencoder architecture enhanced with self-attention layers and further refined for distributional consistency by optimal transport. We validate our Expansive Synthesis by training classifiers on the generated datasets and comparing their performance to classifiers trained on larger, original datasets. Experimental results demonstrate that classifiers trained on synthesized data achieve performance metrics on par with those trained on full-scale datasets, showcasing the model's potential to effectively augment training data. This work represents a significant advancement in data generation, offering a robust solution to data scarcity and paving the way for enhanced data availability in machine learning applications.

Koopcon: A new approach towards smarter and less complex learning

In the era of big data, the sheer volume and complexity of datasets pose significant challenges in machine learning, particularly in image processing tasks. This paper introduces an innovative Autoencoder-based Dataset Condensation Model backed by Koopman operator theory that effectively packs large datasets into compact, information-rich representations. Inspired by the predictive coding mechanisms of the human brain, our model leverages a novel approach to encode and reconstruct data, maintaining essential features and label distributions. The condensation process utilizes an autoencoder neural network architecture, coupled with Optimal Transport theory and Wasserstein distance, to minimize the distributional discrepancies between the original and synthesized datasets. We present a two-stage implementation strategy: first, condensing the large dataset into a smaller synthesized subset; second, evaluating the synthesized data by training a classifier and comparing its performance with a classifier trained on an equivalent subset of the original data. Our experimental results demonstrate that the classifiers trained on condensed data exhibit comparable performance to those trained on the original datasets, thus affirming the efficacy of our condensation model. This work not only contributes to the reduction of computational resources but also paves the way for efficient data handling in constrained environments, marking a significant step forward in data-efficient machine learning.

Implicit Bayes Adaptation: A Collaborative Transport Approach

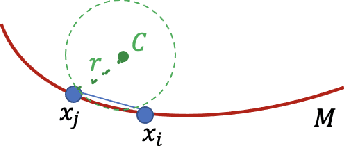
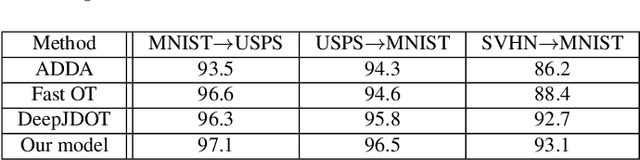
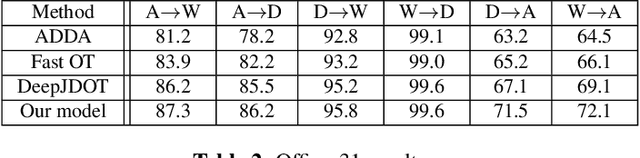
The power and flexibility of Optimal Transport (OT) have pervaded a wide spectrum of problems, including recent Machine Learning challenges such as unsupervised domain adaptation. Its essence of quantitatively relating two probability distributions by some optimal metric, has been creatively exploited and shown to hold promise for many real-world data challenges. In a related theme in the present work, we posit that domain adaptation robustness is rooted in the intrinsic (latent) representations of the respective data, which are inherently lying in a non-linear submanifold embedded in a higher dimensional Euclidean space. We account for the geometric properties by refining the $l^2$ Euclidean metric to better reflect the geodesic distance between two distinct representations. We integrate a metric correction term as well as a prior cluster structure in the source data of the OT-driven adaptation. We show that this is tantamount to an implicit Bayesian framework, which we demonstrate to be viable for a more robust and better-performing approach to domain adaptation. Substantiating experiments are also included for validation purposes.

Refining Self-Supervised Learning in Imaging: Beyond Linear Metric

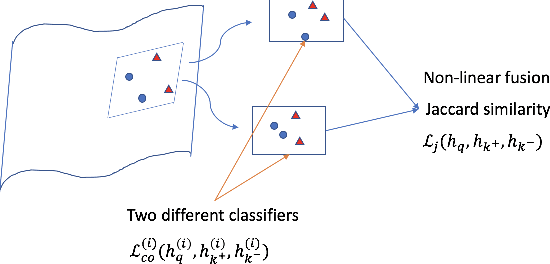
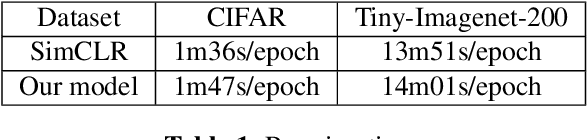
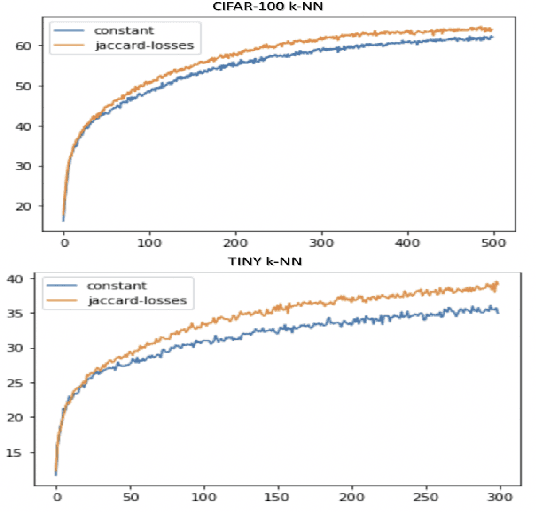
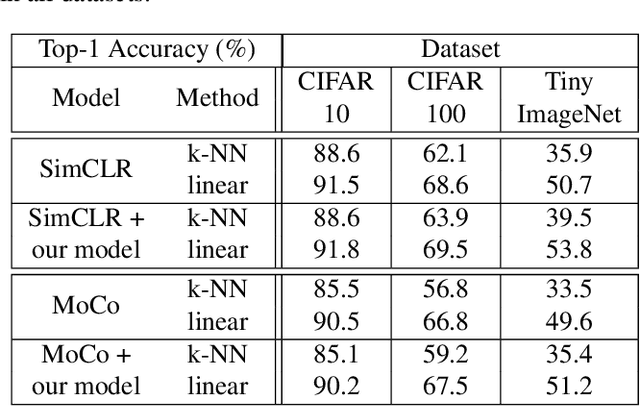
We introduce in this paper a new statistical perspective, exploiting the Jaccard similarity metric, as a measure-based metric to effectively invoke non-linear features in the loss of self-supervised contrastive learning. Specifically, our proposed metric may be interpreted as a dependence measure between two adapted projections learned from the so-called latent representations. This is in contrast to the cosine similarity measure in the conventional contrastive learning model, which accounts for correlation information. To the best of our knowledge, this effectively non-linearly fused information embedded in the Jaccard similarity, is novel to self-supervision learning with promising results. The proposed approach is compared to two state-of-the-art self-supervised contrastive learning methods on three image datasets. We not only demonstrate its amenable applicability in current ML problems, but also its improved performance and training efficiency.